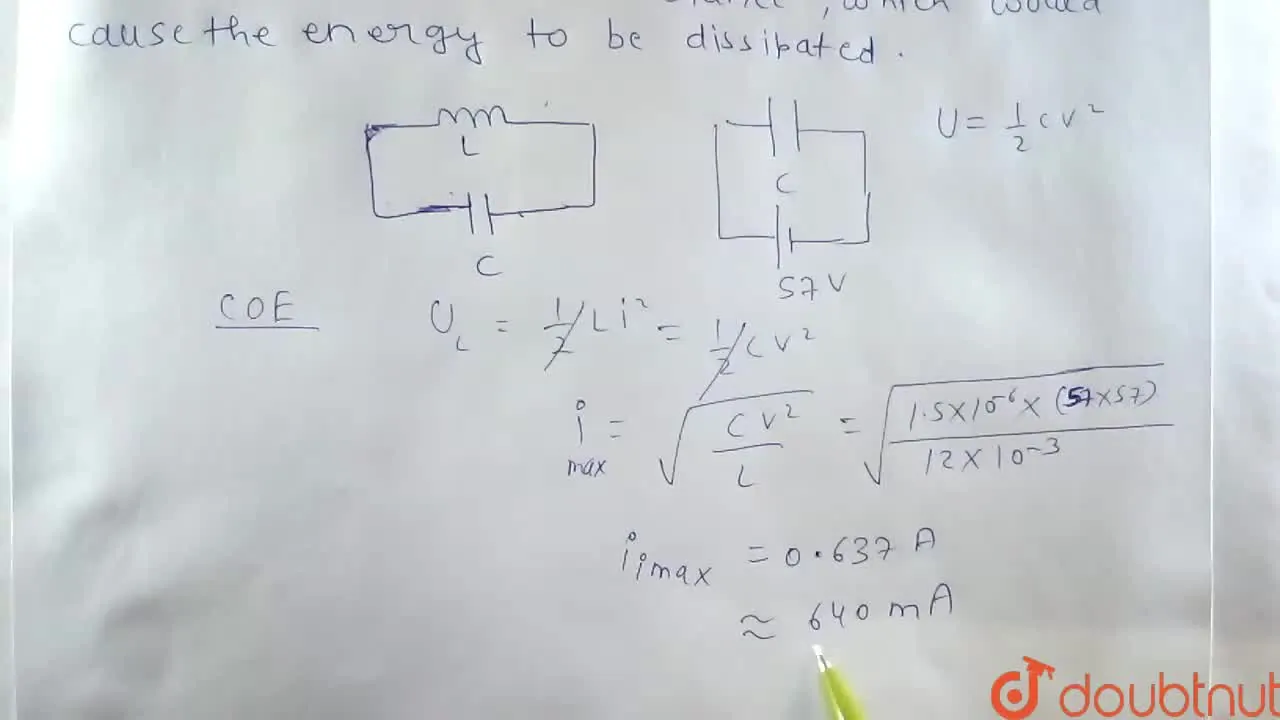A 1.5 μF capacitor is charged to 57 V. The charging battery is then disconnected , and a 12 mH coil is connected in series with the capacitor so that LC oscillations occur. What is the maximum current in the coil ? Assume that the circuit contains no resistance , which woudl cause the energy to be dissipated.
(1)Because the circuit contains no resistance, the electromagnetic energy of the circuit is conserved as the energy is transferred back and forth between the electric field of the capacitor and the magnetic field of the coil (inductor).
(2) At any time t, the energy UB(t) of the magnetic field is related to the current i(t) through the coil by (UB=Li2/2). when all the energy is stored as magnetic energy , the current is at its maximum value I and that energy is UB.max=LI2/2. At any time t, the energy UE(t) of the electric field is related to the charge q(t) on the capacitor by (UE=q2/2C). When all the energy is stored as electrical energy , the charge is at its maximum value Q and that energy is UE.max=Q2/2C.
Calculation:With these ideas, we can now write the conservation of energy as
UB.max=UE.max
or , LI22=Q22C.
Solving for I gives us
I=√Q2LC .
We know L and C , but not Q. However, with (q=CV) we can relate Q to the maximum potential difference V across the capacitor , which is the initial potential difference of 57 V. Thus, substituting Q=CV leads to
I=V√CL=(57V)√1.5×10−6F12×10−3H=0.637A≅ 640 mA
Related Playlists
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT EXERCISE - Check Point8videos
ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT EXERCISE - Problems30videos
ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Integer Type)14videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
ELECTROMAGNETIC WAVES
Similar Questions
A 1.5 μF capacitor is charged to 57V. The charging battery is then disconnected, and a 12 mH coil is connected in series with the capacitor so that LC Oscillations occur. What is the maximum current in the coil? Assume that the circuit has no resistance.
View SolutionA 1μF condenser is charged to 50V. The charging battery is then disconnected and a 10mH coil is connected across capacitor so that the LC oscillations occur. Find the maximum current in the coil?
View SolutionA 1μF condenser is charged to 50V. The charging battery is then disconnected and a 10mH coil is connected across capacitor so that the LC oscillations occur. Find the maximum current in the coil?
View SolutionA 1.5μf capacitor is charged to 20 V. The charging battery is then disconnected and a 15 mH coil is connected in series with the capacitance so that LC oscillations occur. Write current in the inductor as a function of time
View SolutionA 10μF capacitor is charged to a potential of 25 V. The battery is then disconnected and a pure 100 mH coil is connected across the capacitor so that LC oscillations are set-up. What is the maximum current in the coil ?
View SolutionA 1.5μF capacitor is charged to 57 volt.The charging battery is then disconnected and a 12 mH coil is connected across the capacitor so that is zero, what is the maximum value of current in the coil ?
View SolutionA 1.5μF capacitor is charged of 60 V. The charging battery is then disconnected and a 15 mH coil is connected in series with the capacitor so that LC oscillations occur. Assuming that the circuit contains no resistance, the maximum current in this coil shall be close to
View SolutionA 16μF capacitor is charged to 20 volts. The battery is then disconnected and a pure 40mH coil is connected across the capacitor so that LC oscillations are set up. The maximum current in the coil is
View SolutionA 1.5μF capacitor is charged to 20 V. The charging battery is then disconnected , and a 15 mH coil is connected in series with the capacitor so that LC oscillations occur. Write the equation for variation of charge on capacitor and current in the inductor with time taking the instant at which inductor is connected to the capacitor as t=0.
View SolutionA 16 μF capacitor is charged to a 20 Volt potential. Battery is then disconnected and inductor of inductance 40mH is connected across the capacitor, So that LC oscillations are step-up. Maximum current in the coil is
View Solution