A straight horizontal copper wire carries a current i = 30 A. The linear mass density of the wire is 45 g/m. What is the magnitude of the magnetic field needed to balance its weight?

Video Solution

Text Solution

Verified by Experts

(1) Because $\to L$ is directed horizontally (and the current is taken to be positive), Eq. and the right-hand rule for cross products tell us that $\to B$ must be horizontal and rightward to give the required upward ${\to F}_{B}$ .
The magnitude of ${\to F}_{B}$ is $F_{B} = i L B sin ϕ$ Because we want ${\to F}_{B}$ to balance ${\to F}_{g}$ , we want
$i L B sin ϕ = m g$ ,
where mg is the magnitude of ${\to F}_{g}$ and m is the mass of the wire. We also want the minimal field magnitude B for ${\to F}_{B}$ to balance ${\to F}_{g}$ . Thus, we need to maximze $sin ϕ$ in

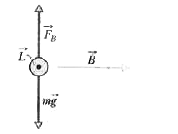
To do so, we set $ϕ = 90^{\circ}$ , thereby arranging for $\to B$ to be perpendicular to the wire. We then have $sin ϕ = 1$ , so yields
We write the result this way because we know m/L, the linear density of the wire. Substituting known data then gives us
$B = \frac{(46.6 \times 10^{- 3} k g / m) (9.8 m / s^{2})}{28 A}$
$= 1.6 \times 10^{- 2} T$
This is about 160 times the strength of Earth.s magnetic field.

Updated on:21/07/2023

Two long, straight, parallel wires are 1.00m apart (as shown in Fig). The upper wire carries a current $I_{1}$ of 6.00A into the plane of the paper.

What is the magnitude of the net field at S?
A $4.1 \times 10^{- 6} T$
B $1.6 \times 10^{- 6} T$
C $3.2 \times 10^{- 6} T$
D $2.1 \times 10^{- 6} T$
Two long, straight, parallel wires are 1.00m apart (as shown in Fig). The upper wire carries a current $I_{1}$ of 6.00A into the plane of the paper.

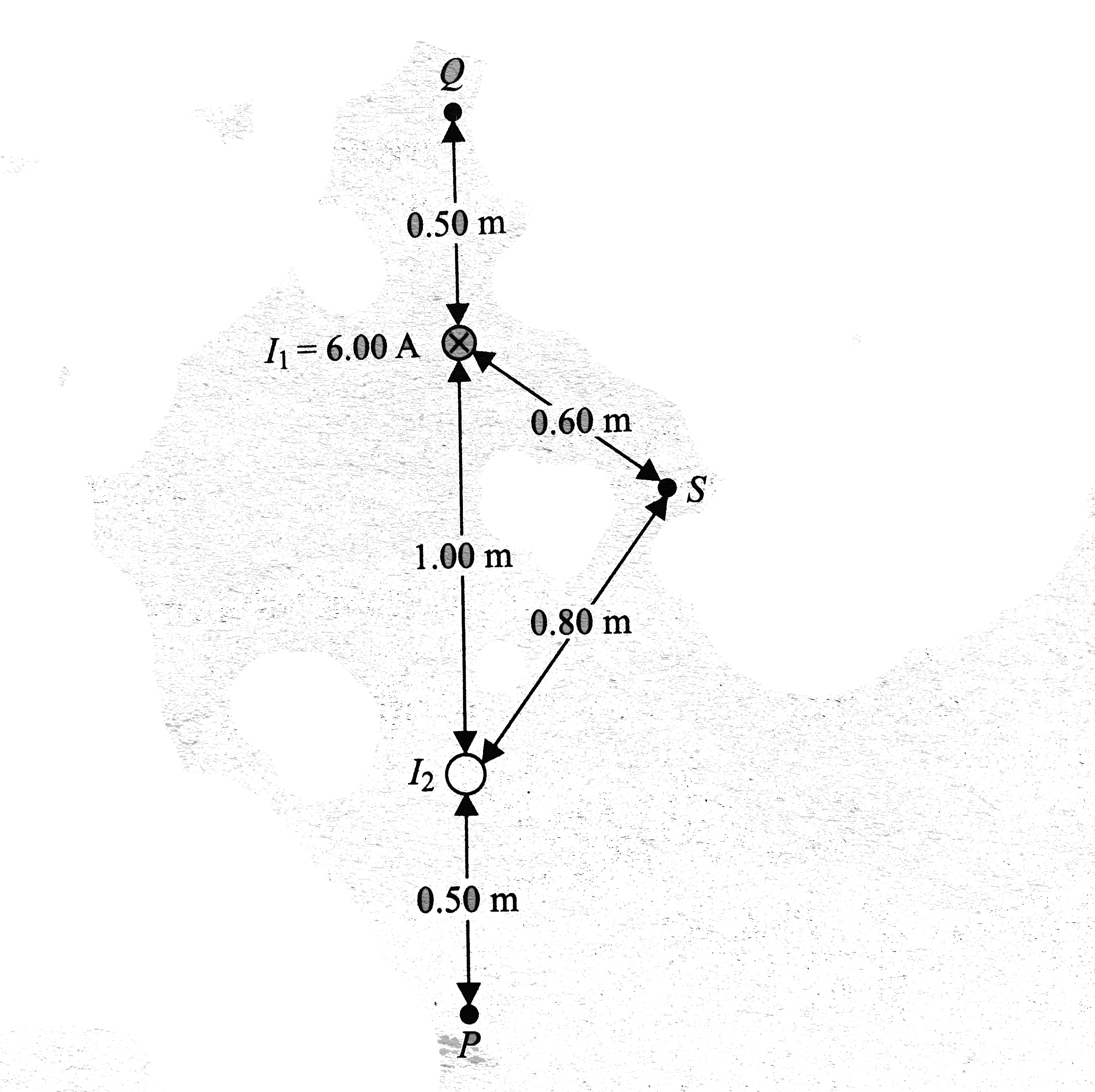
What is the magnitude of the net field at Q?
A $2.13 \times 10^{- 6} T$
B $4.26 \times 10^{- 6} T$
C $1.21 \times 10^{- 6} T$
D $5.30 \times 10^{- 6} T$
A wire carries current toward the north. In the region beneath this wire, What is the direction of the magnetic field due to the current ?
ANorthward
BSouthward
CEastward
DWestward