You have five capacitors To store maximum amount of energy when using a source with terminal voltage V.
You need to connect them all in series
You need to connect them all in parallel
You need to connect three capacitors in parallel and the rest in series with that combination
You need to connect two capacitors in parallel and the rest in series with that combination
The correct Answer is:B
To solve the problem of maximizing energy storage using five capacitors with a fixed terminal voltage V, we can follow these steps:
Step 1: Understand the energy stored in a capacitor
The energy U stored in a capacitor is given by the formula:
U=12CV2
where C is the capacitance and V is the voltage across the capacitor.
Step 2: Analyze the effect of capacitance on energy storage
Since the terminal voltage V is fixed, the energy stored in the capacitors depends only on the capacitance C. To maximize the energy stored, we need to maximize the equivalent capacitance Ceq.
Step 3: Determine the equivalent capacitance for different configurations
1. Series Configuration: For capacitors connected in series, the equivalent capacitance is given by:
1Ceq=1C1+1C2+1C3+⋯
For five identical capacitors (each with capacitance C):
1Ceq=5C⟹Ceq=C5
2. Parallel Configuration: For capacitors connected in parallel, the equivalent capacitance is:
Ceq=C1+C2+C3+⋯
For five identical capacitors:
Ceq=5C
3. Mixed Configurations:
- Three in Parallel and Two in Series: The equivalent capacitance for three capacitors in parallel is:
Ceq1=C+C+C=3C
For the two capacitors in series:
1Ceq2=1C+1C⟹Ceq2=C2
The total equivalent capacitance for this configuration is:
Ctotal=Ceq1+Ceq2=3C+C2=3C+0.5C=3.5C
- Two in Parallel and Three in Series: The equivalent capacitance for two capacitors in parallel is:
Ceq1=C+C=2C
For the three capacitors in series:
1Ceq2=1C+1C+1C⟹Ceq2=C3
The total equivalent capacitance for this configuration is:
Ctotal=Ceq1+Ceq2=2C+C3=2C+0.333C=2.333C
Step 4: Compare the equivalent capacitances
- All in series: Ceq=C5
- All in parallel: Ceq=5C
- Three in parallel and two in series: Ceq=3.5C
- Two in parallel and three in series: Ceq=2.333C
Step 5: Conclusion
The maximum equivalent capacitance occurs when all five capacitors are connected in parallel, yielding Ceq=5C. Therefore, the configuration that stores the maximum amount of energy is when all capacitors are connected in parallel.
Final Answer
The correct option is: Connect all capacitors in parallel.
---
The energy U stored in a capacitor is given by the formula:
U=12CV2
where C is the capacitance and V is the voltage across the capacitor.
Since the terminal voltage V is fixed, the energy stored in the capacitors depends only on the capacitance C. To maximize the energy stored, we need to maximize the equivalent capacitance Ceq.
1. Series Configuration: For capacitors connected in series, the equivalent capacitance is given by:
1Ceq=1C1+1C2+1C3+⋯
For five identical capacitors (each with capacitance C):
1Ceq=5C⟹Ceq=C5
Ceq=C1+C2+C3+⋯
For five identical capacitors:
Ceq=5C
- Three in Parallel and Two in Series: The equivalent capacitance for three capacitors in parallel is:
Ceq1=C+C+C=3C
For the two capacitors in series:
1Ceq2=1C+1C⟹Ceq2=C2
The total equivalent capacitance for this configuration is:
Ctotal=Ceq1+Ceq2=3C+C2=3C+0.5C=3.5C
Ceq1=C+C=2C
For the three capacitors in series:
1Ceq2=1C+1C+1C⟹Ceq2=C3
The total equivalent capacitance for this configuration is:
Ctotal=Ceq1+Ceq2=2C+C3=2C+0.333C=2.333C
- All in series: Ceq=C5
- All in parallel: Ceq=5C
- Three in parallel and two in series: Ceq=3.5C
- Two in parallel and three in series: Ceq=2.333C
The maximum equivalent capacitance occurs when all five capacitors are connected in parallel, yielding Ceq=5C. Therefore, the configuration that stores the maximum amount of energy is when all capacitors are connected in parallel.
The correct option is: Connect all capacitors in parallel.
Topper's Solved these Questions
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
12 Videos
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTIONS (LINKED COMPREHENSION)
8 Videos
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PROBLEMS
48 Videos
- ALL ABOUT ATOMS BOOK - RESNICK AND HALLIDAYCHAPTER - ALL ABOUT ATOMS EXERCISE - CHECKPOINT
1 Video
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )
4 Videos
Similar Questions
You have two identical capacitors and an extermal potential source.
a. Compare the total energy stored in capaciton when they are connected to the applied potential in series and in parallel.
b. Compare the maximum amount of charge stored in each case.
c. Energy storage in a capacitor can be limited by the maximum electric field between the plates. What is the ratio of the electric field for the series for parallel combinations?
View SolutionTwo identical planar capacitor connected in parallel and charged to a voltage U0=12V. When you disconnect them from the voltage source, the distance between the plates of one of the capacitors is reduced to one third of the original distance. What will be the new voltage on the capacitors ?
View Solution
Knowledge Check
In the network given below all the five capacitors have the same capacitance C each . Then the capacitance between the terminal A and B will be
 AC5B5CCCD52 C
AC5B5CCCD52 CA condcuting slab of thickness d2 is inserted between the plates of parallel plate capacitor as shown in the figure . The energy stored in the capacitor when terminals of capacitor are connected across a battery of emf 2V is (plate area is A)
 A2Aε0dV2BAε02dV2CAε0dV2D4Aε0dV2
A2Aε0dV2BAε02dV2CAε0dV2D4Aε0dV2A parallel plate capacitor A is filled with a dielectric whose dielectric constant varies with applied voltage as K = V. An identical capacitor B of capacitance C0 with air as dielectric is connected to voltage source V0=30V and then connected to the first capacitor after disconnecting the voltage source. The charge and voltage on capacitor.
AAare25C0and25VBAare25C0and5VCBare5C0and5VDBare5C0and25V
An oscillating LC circuit consisting of a 1.0 μF capacitor and a 9.0 mH coil has a maximum voltage of 3.0 V. What are (a) the maximum charge on the capacitor, (b) the maximum current through the circuit, and (c) the maximum energy stored in the magnetic field of the coil?
View SolutionThe voltage applied across a capacitor having a capacitance of 10μF is varies as shown in figure:
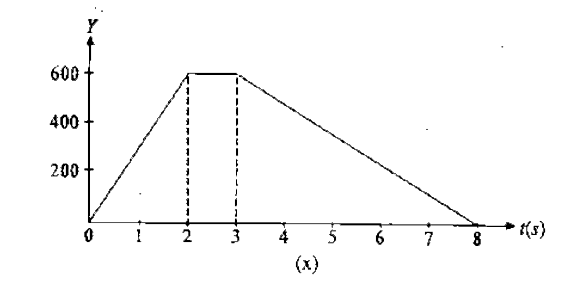
At the time instant when the terminal voltage across capacitor is 600V calculate
(a) The charge on capacitor ltBrgt (b) The energy stored in the capacitor
(c) Draw the curve of current in connecting wires as a function of time.
View SolutionCalculate energy stored in a capacitor stored in a capacitor of 5μF when it is charged to a potential of 250 volt.
View SolutionThe figure shows a network of five capacitors connected to a 100 V supply, Calculate the total energy stored in the network.
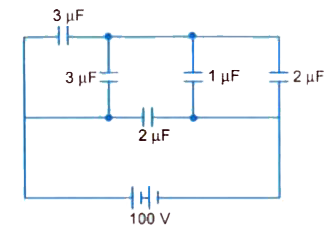
View SolutionA capacitor of capacitance C1=1μF can withstand maximum voltage V1=6kV and another capacitor of capacitance C2=3μF can withstand maximum voltage V24kV. When the two capacitors are connected in series, the combined system can withstand a maximum voltage of
View Solution
