A battery of potential V stores charge q on a combination of two identical capacitors. What are the potential difference across the end the charge or either capacitors if the capacitors are (a) in parallel and (b) in series?
To solve the problem of finding the potential difference across the ends of two identical capacitors when connected to a battery of potential V, we will consider two scenarios: (a) when the capacitors are connected in parallel and (b) when they are connected in series.
1. Understanding the Configuration:
- When two capacitors are connected in parallel, they share the same voltage across their terminals.
2. Voltage Across Each Capacitor:
- The potential difference (voltage) across each capacitor will be equal to the voltage of the battery. Therefore, the voltage across each capacitor (V1 and V2) is:
V1=VandV2=V
3. Charge on Each Capacitor:
- The charge stored in a capacitor is given by the formula:
Q=C⋅V
- Since the capacitors are identical and connected in parallel, the total charge (Q) is the sum of the charges on both capacitors:
Q=Q1+Q2
- Since both capacitors have the same capacitance (C), we can express the charges as:
Q1=C⋅VandQ2=C⋅V
- Thus, the total charge becomes:
Q=C⋅V+C⋅V=2C⋅V
4. Final Charge Distribution:
- Each capacitor will have half of the total charge:
Q1=Q2=Q2
(b) Capacitors in Series:
1. Understanding the Configuration:
- When two capacitors are connected in series, the same charge (Q) flows through both capacitors.
2. Voltage Across Each Capacitor:
- The total voltage across the series combination is the sum of the voltages across each capacitor:
V=V1+V2
3. Voltage Across Each Capacitor:
- The voltage across each capacitor can be expressed as:
V1=QCandV2=QC
- Therefore, the total voltage can be written as:
V=QC+QC=2⋅QC
4. Solving for Voltage:
- Rearranging gives:
QC=V2
- Thus, the voltage across each capacitor is:
V1=V2=V2
Summary of Results:
- For capacitors in parallel:
- Voltage across each capacitor: V1=V, V2=V
- Charge on each capacitor: Q1=Q2=Q2
- For capacitors in series:
- Voltage across each capacitor: V1=V2=V2
- Charge on each capacitor: Q1=Q2=Q
- When two capacitors are connected in parallel, they share the same voltage across their terminals.
- The potential difference (voltage) across each capacitor will be equal to the voltage of the battery. Therefore, the voltage across each capacitor (V1 and V2) is:
V1=VandV2=V
- The charge stored in a capacitor is given by the formula:
Q=C⋅V
- Since the capacitors are identical and connected in parallel, the total charge (Q) is the sum of the charges on both capacitors:
Q=Q1+Q2
- Since both capacitors have the same capacitance (C), we can express the charges as:
Q1=C⋅VandQ2=C⋅V
- Thus, the total charge becomes:
Q=C⋅V+C⋅V=2C⋅V
- Each capacitor will have half of the total charge:
Q1=Q2=Q2
- When two capacitors are connected in series, the same charge (Q) flows through both capacitors.
- The total voltage across the series combination is the sum of the voltages across each capacitor:
V=V1+V2
- The voltage across each capacitor can be expressed as:
V1=QCandV2=QC
- Therefore, the total voltage can be written as:
V=QC+QC=2⋅QC
- Rearranging gives:
QC=V2
- Thus, the voltage across each capacitor is:
V1=V2=V2
- For capacitors in parallel:
- Voltage across each capacitor: V1=V, V2=V
- Charge on each capacitor: Q1=Q2=Q2
- Voltage across each capacitor: V1=V2=V2
- Charge on each capacitor: Q1=Q2=Q
Topper's Solved these Questions
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PROBLEMS
48 Videos
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
23 Videos
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)
3 Videos
- ALL ABOUT ATOMS BOOK - RESNICK AND HALLIDAYCHAPTER - ALL ABOUT ATOMS EXERCISE - CHECKPOINT
1 Videos
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )
4 Videos
Similar Questions
A battery is used to charge a parallel plate combination of two identical capacitors. If the potential difference across the battery is V and the total charge Q flows through the battery during the charging process then 1) The charge on each capacitor is Q/2 and the potential of each capacitor is V/2 2) The charge on each capacitor is Q and the potential of each capacitor is V 3) The charge on each capacitor is Q/2 and the potential of each capacitor is V 4) The charge on each capacitor is Q and the potential of each capacitor is V/2
View SolutionFind charge on each capacitor and potential difference across each capacitor .

View Solution
Knowledge Check
A capacitor C is charged to a potential difference V and battery is disconnected. Now if the capacitor plates are brough close slowely by some distance:
Asome +ve work is done by external agentBenegry of capacitor will decreaseCenegry of capacitor will increaseDnone of the aboveA 10V battery is connected to two capacitors C1 and C2 and a resistor R. When the capacitors are fully charged, then the potential difference across the resistor will be
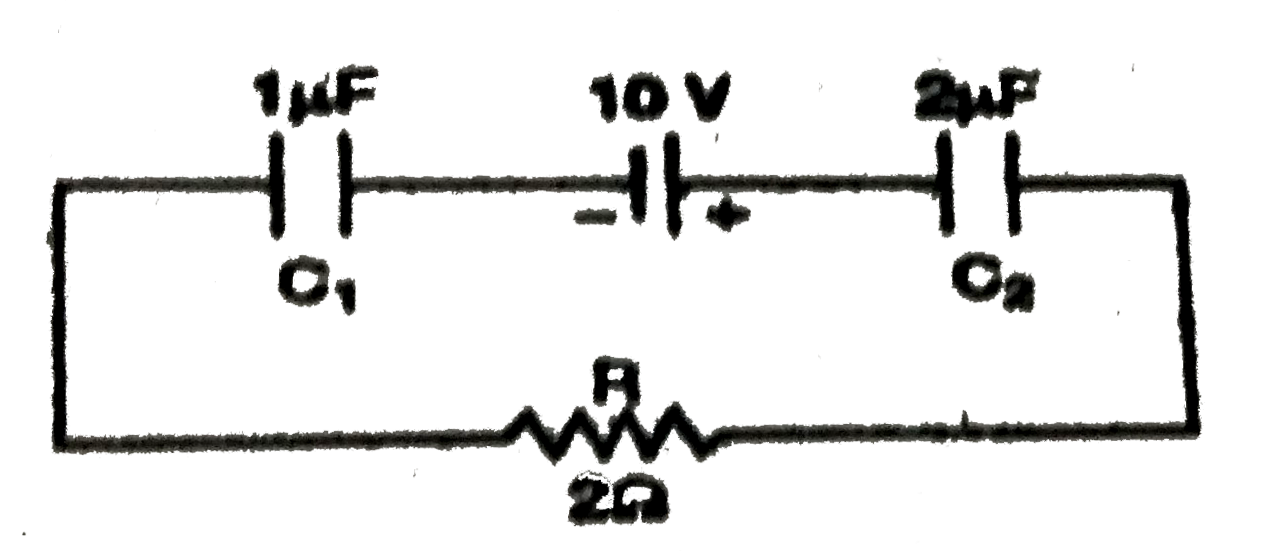 A10 VB5VC3.33 VDzero
A10 VB5VC3.33 VDzeroTwo identical capacitors are connected in series with a source of constant voltage V. If Q is the charge on one of the capacitors, the capacitance of each capacitor is :
AQ/2VBQ/VC2Q/VDNone of these
The charge stored in a capacitor is 20μ C and the potential difference across the plates is 500V .Its capacity is ..?
View SolutionIf A is connerted with D and B is connected with C find the potential difference a across each capacitor and the final charge in each capacitor.
View SolutionA 100pF capacitor is charged to a potential difference of 80.0V and the charging battery is disconnected. The capacitor is then connected in parallel with a second capacitor. If the potential difference across the first capacitor drops to 35.0 V what is the capacitance of this second capacitor?
View SolutionTwo capacitors of capacitance 6uF and 4uF are put in series across a 120V battery. What is the potential difference across the 4uF capacitor?
View SolutionPlot A&B represent variation of charge with potential difference across the combination (series and parallel) of two capacitors. Then Find the values of capacitance of capacitors.
_2019_CBT5_E01_040_Q01.png)
View Solution
