In Fig. 5-23a, a cord pulls a box of sea biscuits up along a frictionless plane inclined at angle θ=30.0∘. The box has mass m = 5.00 kg, and the force from the cord has magnitude T = 25.0 N. What is the box's acceleration a along the inclined plane ?
To find the acceleration of the box along the inclined plane, we will use Newton's second law of motion. Let's break down the steps:
Step 1: Identify the forces acting on the box
The forces acting on the box are:
1. The tension (T) in the cord pulling the box up the incline, which is given as T=25.0N.
2. The gravitational force acting downward, which can be decomposed into two components:
- Perpendicular to the incline: mgcos(θ)
- Parallel to the incline: mgsin(θ)
Step 2: Calculate the gravitational force components
Given:
- Mass of the box, m=5.00kg
- Gravitational acceleration, g=9.81m/s2
- Angle of incline, θ=30.0∘
The weight of the box is:
mg=5.00kg×9.81m/s2=49.05N
Now, calculate the component of the weight acting down the incline:
mgsin(θ)=49.05N×sin(30∘)=49.05N×0.5=24.525N
Step 3: Apply Newton's second law
According to Newton's second law:
Fnet=ma
Where Fnet is the net force acting on the box along the incline.
The net force acting on the box is:
Fnet=T−mgsin(θ)
Substituting the values:
Fnet=25.0N−24.525N=0.475N
Step 4: Calculate the acceleration
Now, we can find the acceleration a using:
a=Fnetm
Substituting the values:
a=0.475N5.00kg=0.095m/s2
Final Answer
The acceleration of the box along the inclined plane is:
a=0.095m/s2
The forces acting on the box are:
1. The tension (T) in the cord pulling the box up the incline, which is given as T=25.0N.
2. The gravitational force acting downward, which can be decomposed into two components:
- Perpendicular to the incline: mgcos(θ)
- Parallel to the incline: mgsin(θ)
Given:
- Mass of the box, m=5.00kg
- Gravitational acceleration, g=9.81m/s2
- Angle of incline, θ=30.0∘
mg=5.00kg×9.81m/s2=49.05N
mgsin(θ)=49.05N×sin(30∘)=49.05N×0.5=24.525N
According to Newton's second law:
Fnet=ma
Where Fnet is the net force acting on the box along the incline.
Fnet=T−mgsin(θ)
Substituting the values:
Fnet=25.0N−24.525N=0.475N
Now, we can find the acceleration a using:
a=Fnetm
Substituting the values:
a=0.475N5.00kg=0.095m/s2
The acceleration of the box along the inclined plane is:
a=0.095m/s2
Topper's Solved these Questions
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - CHECKPOINT
5 Videos
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PROBLEMS
52 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (Integer Type )
5 Videos
- FORCE AND MOTION-IIBOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
1 Videos
Similar Questions
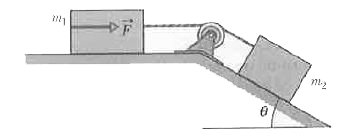
Figure 5-59 shows a box of mass m2=1.0 kg on a friction-less plane inclined at angle θ=30∘. It is connected by a cord of negligible mass to a mass m1=2.5 kg on a horizontal frictionless surface. The pulley is frictionless and massless. (a) If the magnitude of horizontal force →F is 2.3 N, what is the tension in the connecting cord? (b) What is the largest value the magnitude of →F may have without the cord becoming slack?
View SolutionA block of mass m1=3.70 kg on a frictionless plane inclined at angle 30.0∘ is connected by a cord over a massless, frictionless pulley to a second block of mass m2=2.30 kg (see Fig. 5-32).
(a) What is the magnitude of the acceleration of each block?
(b) What is the direction of the acceleration of the hanging block ?
(c) What is the tension in the cord?
View Solution
Knowledge Check
A block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
AmgBmgcosθCmgcosθDmgtanθA person pushes a block of mass 4 kg up a frictionless inclined plane 10 m long and that makes an angle of 30∘ with the horizontal . Then the work done is
A33.5JB−392JC339.4JD−196JA very heavy box is kept on a frictionless incline plane inclined at an angle θ from the horizontal. Box is having an another frictionless incline plane, inclined plane as shown in the figure. A block of mass m is kept on this inclined plane inside the box. Acceleration of block w.r.t. box is
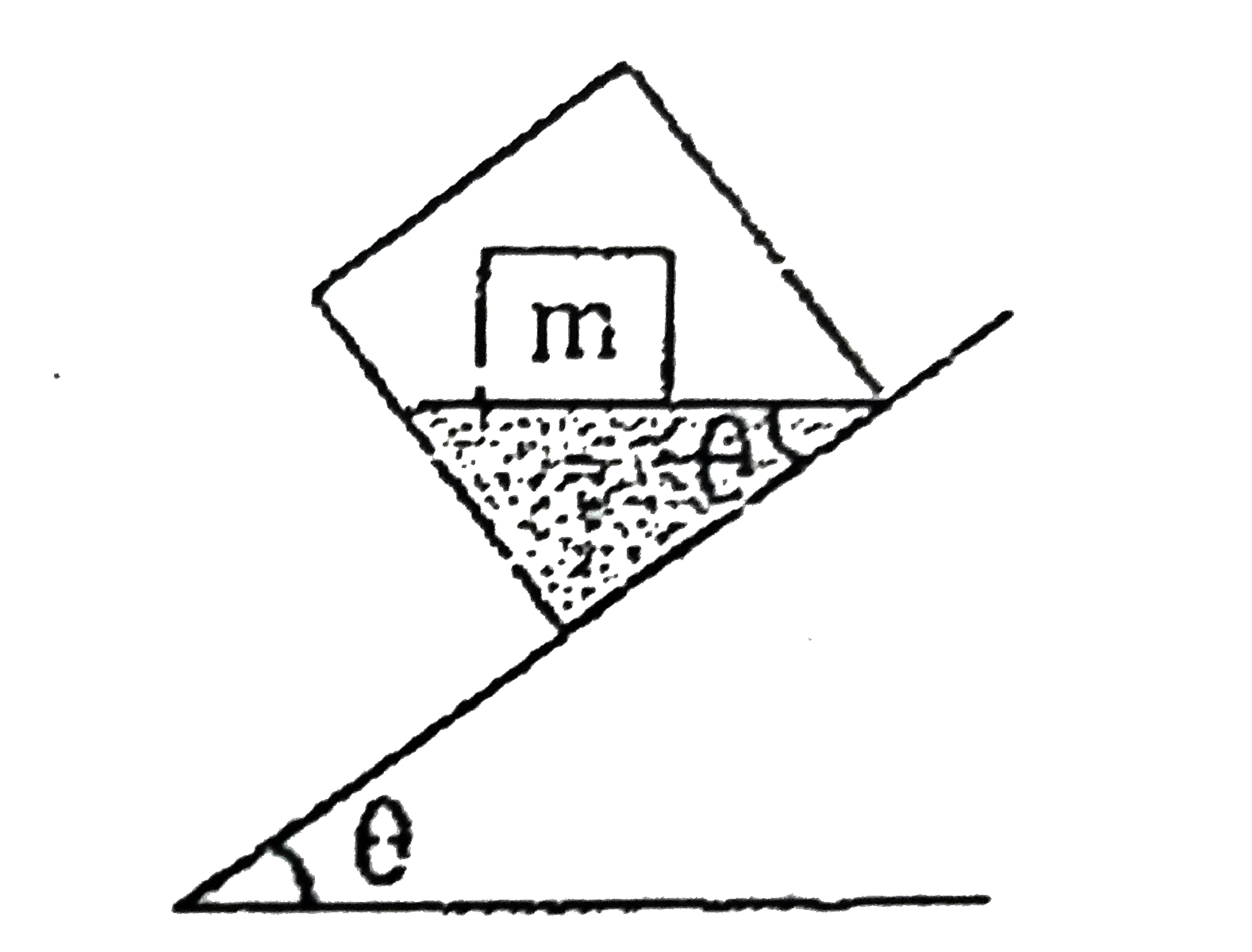 Agsin2θBgcos2θCgsinθcosθDzero
Agsin2θBgcos2θCgsinθcosθDzero
A 20kg box is gently placed on a rough inclined plane of inclination 30∘ with horizontal. The coefficient of sliding friction between the box and the plane is 0.5.Find the acceleration of the box down the incline.
View SolutionA drum of radius R and mass M rolls down without slipping along an inclined plane of angle θ. The frictional force
View SolutionA body is projected up along a rough inclined plane of inclination 45∘ . The coefficient of friction is 0.5. Then the retardation of the block is
View SolutionThe work done in sliding a wooden box of mass 5 kg along a friction less inclined plane of inclination 30∘ and length 10 m is ______J. (g=10ms−2)
View SolutionA block of mass 10kg is pushed up on a smooth incline plane of inclination 30∘, so that it has acceleration 2m/s2. The applied force is
View Solution
