व्यासार्ध के वृत्ताकार स्थान में एकसमान परन्तु समय के साथ परिवर्तित होने वाला चुम्बकीय क्षेत्र B(t) है और यह पृष्ठ के तल की ओर है जैसा कि चित्र IV.18 में दिखाया गया है। वृत्ताकार स्थान के केन्द्र से r दूरी पर किसी बिन्दु P पर प्रेरित वैद्युत क्षेत्र का परिमाण
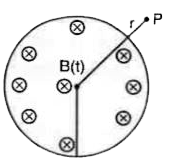
शून्य है।
1/r के अनुसार घटता है।
r के अनुसार बढ़ता है।
1/r2 के अनुसार घटता है।
The correct Answer is:b
∮→E.→dl=dϕBdt=ddt(→B.→A)=AdBdt=(πa2)dBdt
क्योंकि ∮→E.→dl=E(2πr), इसलिए E(2πr)=πa2(dBdt)
या E=(a22r)dBdt या E∝1r
Topper's Solved these Questions
- प्रत्यावर्ती धाराएँ BOOK - GRB PUBLICATION HINDICHAPTER - प्रत्यावर्ती धाराएँ EXERCISE - प्रतियोगिता सामग्री ( बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प )
10 Videos
- प्रत्यावर्ती धाराएँ BOOK - GRB PUBLICATION HINDICHAPTER - प्रत्यावर्ती धाराएँ EXERCISE - पैरा-आधारित बहुविकल्पीय बोधात्मक प्रश्न पैरा 1
3 Videos
- प्रत्यावर्ती धाराएँ BOOK - GRB PUBLICATION HINDICHAPTER - प्रत्यावर्ती धाराएँ EXERCISE - NCERT पाठ्यपुस्तक अभ्यास : उत्तरों सहित
15 Videos
- प्रकाशिक यन्त्रBOOK - GRB PUBLICATION HINDICHAPTER - प्रकाशिक यन्त्रEXERCISE - NCERT पाठ्यपुस्तक अभ्यास
8 Videos
- विद्युत परिपथ , विद्युत ऊर्जा और शक्ति BOOK - GRB PUBLICATION HINDICHAPTER - विद्युत परिपथ , विद्युत ऊर्जा और शक्ति EXERCISE - प्रतियोगिता सामग्री ( रिक्त स्थान भरना )
15 Videos
Similar Questions
एक चालक लूप किसी एकसमान चुम्बकीय क्षेत्र में ऐसे रखा जाता है कि इसका तल क्षेत्र पर लम्बवत हो। लूप में विद्युत वाहक बल प्रेरित होता है यदि
View Solutionजब l लम्बाई का एक चालक,ab R प्रतिरोध वाले U-आकार के चालक के ऊपर v वेग से चलाया जाता है, तो गतिक विद्युत वाहक बल ε चालक के सिरों पर प्रेरित हो जाता है। परिपथ में धारा, चित्र IV.32 में दिखाए अनुसार बहती है। चालक, पृष्ठ के तल में अन्दर की ओर काम कर रहे चुम्बकीय क्षेत्र B में चल रहा है। उपरोक्त के आधार पर निम्न प्रश्नों के सबसे उपयुक्त उत्तर चुनें:
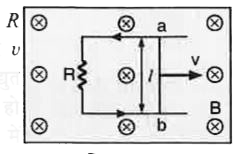
चालक ab को स्थिर वेग v से चलाने के लिए आवश्यक बल है :
View Solution100Ωका प्रतिरोधक 220V,50Hzac आपूर्ति से जोड़ा जाता है।
(a) परिपथ में धारा का rms मान कितना है?
(b) एक पूरे चक्र में व्यय हुई नेट शक्ति कितनी है?
View Solutionएक छोटे दूरदर्शक के अभिदृश्यक लेन्स की फोकस दुरी 144cm , और नेत्रिका की 6.0cm है। दूरदर्शक की आवर्धन क्षमता क्या है ? अभिदृश्यक और नेत्रिका के बीच कितनी दुरी है ?
View Solutionएक H-परमाणु में एक इलेक्ट्रॉन नाभिक के इर्द-गिर्द 6.6×1015 rps लगाता है। तुल्य धारा ..............A है।
View Solutionएकसमान विद्युत क्षेत्र E=3×103ˆi(N)/C पर विचार कीजिये ।
(a) इस क्षेत्र का 10 cm भुजा के वर्ग के उस पार्श्व से जिसका तल yz तल के समांतर है, गुजरने वाला फ्लक्स क्या है ?
(b) इस वर्ग से गुजरने वाला फ्लक्स कितना है यदि इसके तल का अभिलंब x- अक्ष से 60∘ कोण बनता है ?
View Solutionचित्र में दिखाए गए छायांकित क्षेत्र के लिए असामिका है-
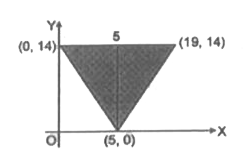
View Solutionवृत्ताकार धारावाही कुंडली के कारण चुम्बकीय क्षेत्र
View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष पर चुंबकीय क्षेत्र
View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष तथा केन्द्र पर चुंबकीय क्षेत्र | ऐम्पियर का परिपथीय नियम
View Solutionधारावाही वृत्ताकार लूप और कुंडली के केंद्र पर चुंबकीय क्षेत्र
View Solutionधारावाहिक चाप के कारण चुंबकीय क्षेत्र|वृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionवृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र|धारावाहि चाप के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionविद्युत धारावाही वृत्ताकार पाश के केन्द्र पर चुंबकीय क्षेत्र
View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष पर चुंबकीय क्षेत्र
View Solutionधारावाही वृत्ताकार लूप और कुंडली के अक्ष पर चुंबकीय क्षेत्र
View Solution
