बराबर विधुत वाहक बल के दो स्त्रोत एक बाहरी प्रतिरोध R के साथ जोड़े होते हैं। दोनों स्त्रोतों के आन्तरिक प्रतिरोध और हैं। यदि आन्तरिक प्रतिरोध वाले स्रोत के सिरों पर विभवान्तर शून्य हो, तो
The correct Answer is:D
क्योंकि इसलिए
फिर क्योंकि इसलिए
जहाँ से .
Topper's Solved these Questions
- विद्युत परिपथ , विद्युत ऊर्जा और शक्ति Book:GRB PUBLICATION HINDIChapter:विद्युत परिपथ , विद्युत ऊर्जा और शक्ति Exercise:प्रतियोगिता सामग्री ( कॉलम मिलाना )
Explore 4 Videos
- विद्युत परिपथ , विद्युत ऊर्जा और शक्ति Book:GRB PUBLICATION HINDIChapter:विद्युत परिपथ , विद्युत ऊर्जा और शक्ति Exercise:प्रतियोगिता सामग्री ( कथन-कारण-आधारित प्रश्न )
Explore 12 Videos
- विद्युत परिपथ , विद्युत ऊर्जा और शक्ति Book:GRB PUBLICATION HINDIChapter:विद्युत परिपथ , विद्युत ऊर्जा और शक्ति Exercise:NCERT पाठ्य-पुस्तक अभ्यास : उत्तरों सहित
Explore 8 Videos
- प्रत्यावर्ती धाराएँ Book:GRB PUBLICATION HINDIChapter:प्रत्यावर्ती धाराएँ Exercise:रिक्त स्थान भरना
Explore 15 Videos
- वैद्युत क्षेत्र और गाउस नियमBook:GRB PUBLICATION HINDIChapter:वैद्युत क्षेत्र और गाउस नियमExercise:NCERT पाठ्यपुस्तक अभ्यास : उत्तरो सहित
Explore 29 Videos
Similar Questions
कॉलम-I में दिए गए चालकों के गुणों का कॉलम-II में दी गई राशियों से मिलान करें।
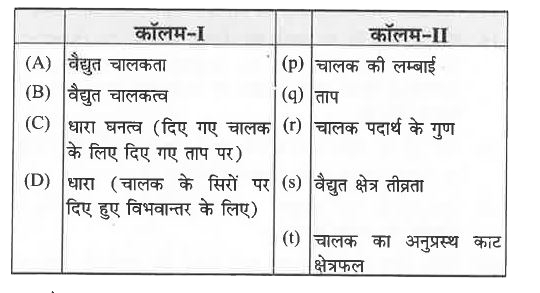
View SolutionA : बड़े शुष्क सेल का विधुत वाहक बल ज्यादा होता है।
R : शुष्क सेल का विधुत वाहक बल, इसके साइज़ पर निर्भर करता है
View Solutionएक कार की संचायक बैटरी का विधुत वाहक बल10 V है। यदि बैटरी का आन्तरिक प्रतिरोध 0.4Ω हो, तो बैटरी से अधिकतम कितनी धारा ली जा सकती है ?
View Solutionएक शुद्ध प्रेरकत्व में क्षयित हुई औसत शक्ति.........।
View Solutionहवा में एक दूसरे से 30 cm दूर रने 2×10−7C और 3×10−7C आवेश वाले दो छोटे आवेशित गोलों के बीच बल ज्ञात करें।
View Solutionshow that r2r3+r3r1+r1r2=s2
View SolutionProve that r1(r2+r3)√r1r2+r2r3+r3r1=a
View SolutionStatement-1: ln !ABC,r1+r2+r3−r=4R
Statement-2: In !ABC,r1r2+r2r3+r3r1=!2
View SolutionProve the questions
a(rr1+r2r3)=b(rr2+r3r1)=c(rr3+r1r2)
View SolutionStatement 1: in a ΔABC if a<b<c and r inradius and r1,r2,r3 are the exradii opposite to angle r>r1>r2>r3 respectively then
Statement 2: For , ΔABCr1r2+r2r3+r3r1=r1r2r3r
View SolutionThe magnitudes of the gravitational fields at distances r1 and r2 from the centre of a uniform sphere of radius R and mass M are F1 and F2 respectively then
(a) F1F2=r1r2 if r1<R and r2<R
(b) F1F2=(r2r1)2 if r1>R and r2>R
(c) F1F2=r1r2 if r1>R and r2>R
(d) F1F2=(r1r2)2 if r1<R and r2<R
View SolutionThe magnitudes of the gravitational fields at distances r1 and r2 from the centre of a uniform sphere of radius R and mass M are F1 and F2 respectively then
(a) F1F2=r1r2 if r1<R and r2<R
(b) F1F2=(r2r1)2 if r1>R and r2>R
(c) F1F2=r1r2 if r1>R and r2>R
(d) F1F2=(r1r2)2 if r1<R and r2<R
View SolutionThe magnitude of gravitational field at distances r_(1) and r_(2) from the center of a uniform sphere of radius R and mass M are respectively I_(1) and I_(2) . The ratio I_(1)//I_(2) is given in the column II. Make correct matching {:("Column-I",,"Column-II"),((A) r_(1) gt R and r_(2) gt R,,(P) (r_(1)r_(2)^(2))/(R_(3))),((B) r_(1) lt R and r_(2) gt R,,(Q) (R_(3))/(r_(2)r_(1)^(2))),((C) r_(1) gt R and r_(2) lt R,,(R) (r_(1))/(r_(2))),((D) r_(1) lt R and r_(2) gt R,,(S)(r_(2)^(2))/(r_(1)^(2))):}
View SolutionIf rr2=r1r3 then
View Solutionr+r3+r1−r2=
View SolutionThe conbined resistance R of two resistors R,& R2(R1,R2>0) is given by . 1R=1R1+1R2. If R1+R2= constant Prove that the maximum resistance R is obtained by choosing R1=R2
View Solution