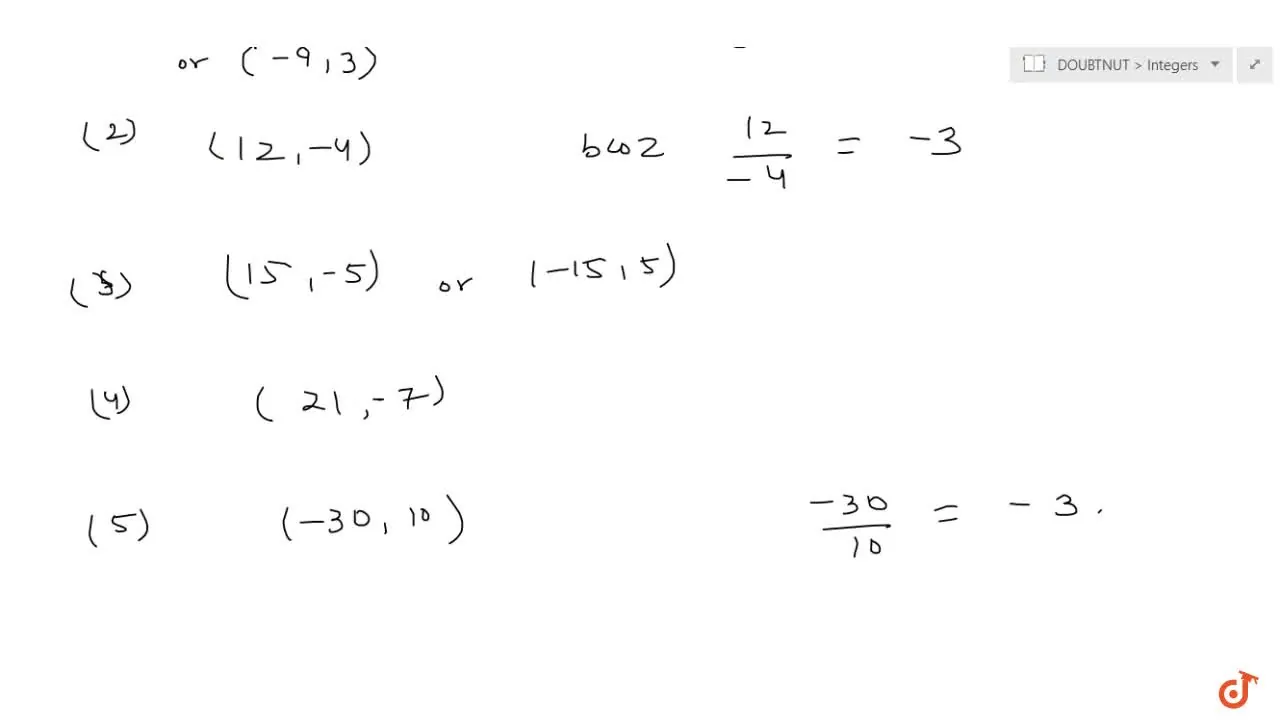Write five pairs of integers (a,b) such that a÷b=−3. One such pair is (6−2). Because 6÷(−2)=(−3) .
a)(9,-3)
b)(12,-4)
c)(15,-5)
d)(18,-6)
e)(21,-7).
Related Playlists
- BOOK - NCERTCHAPTER - INTEGERSEXERCISE - EXERCISE 1.38videos
INTEGERS
- BOOK - NCERTCHAPTER - INTEGERSEXERCISE - EXERCISE 1.110videos
INTEGERS
- BOOK - NCERTCHAPTER - FRACTIONS AND DECIMALSEXERCISE - EXERCISE 2.65videos
FRACTIONS AND DECIMALS
- BOOK - NCERTCHAPTER - LINES AND ANGLESEXERCISE - SOLVED EXAMPLES1videos
LINES AND ANGLES
Similar Questions
The number of positive integer pairs (a, b) such that ab - 24 = 2b is
View SolutionFind the sum of the pairs of integers :
−6−4View SolutionIf ?is an operation on integers such that a?b= −a+b−(−2) for all integers a, b . Find the value of 4?3 (ii) (−2)?(−3) 6?(−5) (iv) (−5)?6
View SolutionDetermine the number of ordered pairs of positive integers (a , b) such that the atleast common multiple of a and b is 23571113 .
View SolutionWrite the order pair (2,−3) in the form of (a+ib).
View SolutionIf a+b=10, then the ordered pair (a,b) such that a3b2 is maximum, is
View SolutionWrite the conjugate pair of √3−√6 .
View SolutionThe number of positive integral ordered pairs of (a,b) such that 6,a,b are in harmonic progression is _________.
View SolutionThe number of pairs of relatively prime positive integers (a, b) such that ab+15b4a is an integer is
View SolutionThe number of ordered pairs (a,b) of positive integers such that2a−1b and 2b−1a are both integers is
View Solution