Prove that: [(vecaxxvecb)xx(vecaxxvecc)].vecd=pveca vecb vecc](veca.vecd)
[→a→b→c](→c.→d)
[→a→b→c](→a.→d)
[(→a,→b,→c)[(→c.→d)
none of these
The correct Answer is:B
NA
Topper's Solved these Questions
- SCALAR AND VECTOR PRODUCTS OF THREE VECTORS Book:OBJECTIVE RD SHARMAChapter:SCALAR AND VECTOR PRODUCTS OF THREE VECTORS Exercise:Section II - Assertion Reason Type
Explore 12 Videos
- REAL FUNCTIONS Book:OBJECTIVE RD SHARMAChapter:REAL FUNCTIONS Exercise:Chapter Test
Explore 60 Videos
- SCALER AND VECTOR PRODUCTS OF TWO VECTORS Book:OBJECTIVE RD SHARMAChapter:SCALER AND VECTOR PRODUCTS OF TWO VECTORS Exercise:Section I - Solved Mcqs
Explore 12 Videos
Similar Questions
Prove that: [(→a×→b)×(→a×→c)].→d=[→a→b→c](→a.→d)
View SolutionProve that →a×{→b×(→c×→d)}=(→b.→d)(→a×→c)−(→b.→c)(→a×→d)
View SolutionProve that: (→a×→b)×(→c×→d)+(→a×→c)×(→d×→b)+(→a×→d)×(→b×→c)=2[→b→c→d]→a
View SolutionIf →a,→baand→c are non- coplanar vecotrs, then prove that ∣∣(→a.→d)(→b×→c)+(→b.→d)(→c×→a)+(→c.→d)(→a×→b) is independent of →d where →d is a unit vector.
View SolutionIf →a,→baand→c are non- coplanar vecotrs, then prove that ∣∣(→a.→d)(→b×→c)+(→b.→d)(→c×→a)+(→c.→d)(→a×→b) is independent of →d where →d is a unit vector.
View Solutionfor any four vectors →a,→b,→cand→d prove that →d.(→a×(→b×(→c×→d)))=(→b.→d)[→a→c→d]
View Solutionfor any four vectors →a,→b,→cand→d prove that →d.(→a×(→b×(→c×→d)))=(→b.→d)[→a→c→d]
View SolutionIf →a,→b,→c,→d are the position vectors of the verticles of a cyclic quadrilateral ABCd prove that
∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)+∣∣→b×→c+→c×→d+→d×→b∣∣(→b−→c).(→d−→c)=0
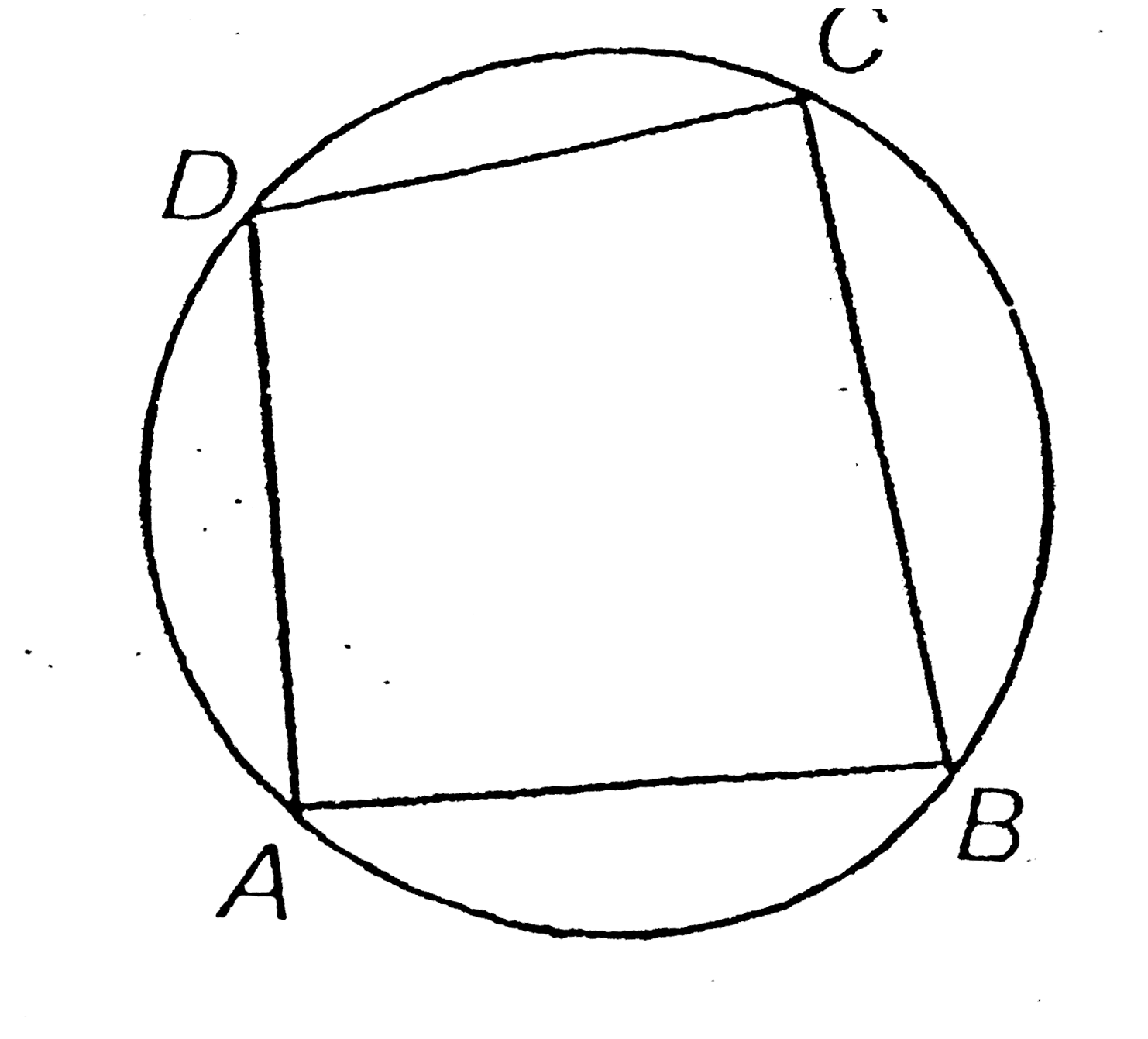
View SolutionIf →a,→b,→cand→d are the position vectors of the vertices of a cycle quadrilateral ABCD, prove that ∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)+∣∣→b×→c+→c×→d+→d+→d×→b∣∣(→b−→c).(→d−→c)
View SolutionIf →a,→b,→cand→d are the position vectors of the vertices of a cycle quadrilateral ABCD, prove that ∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)+∣∣→b×→c+→c×→d+→d+→d×→b∣∣(→b−→c).(→d−→c)
View Solution

