Question

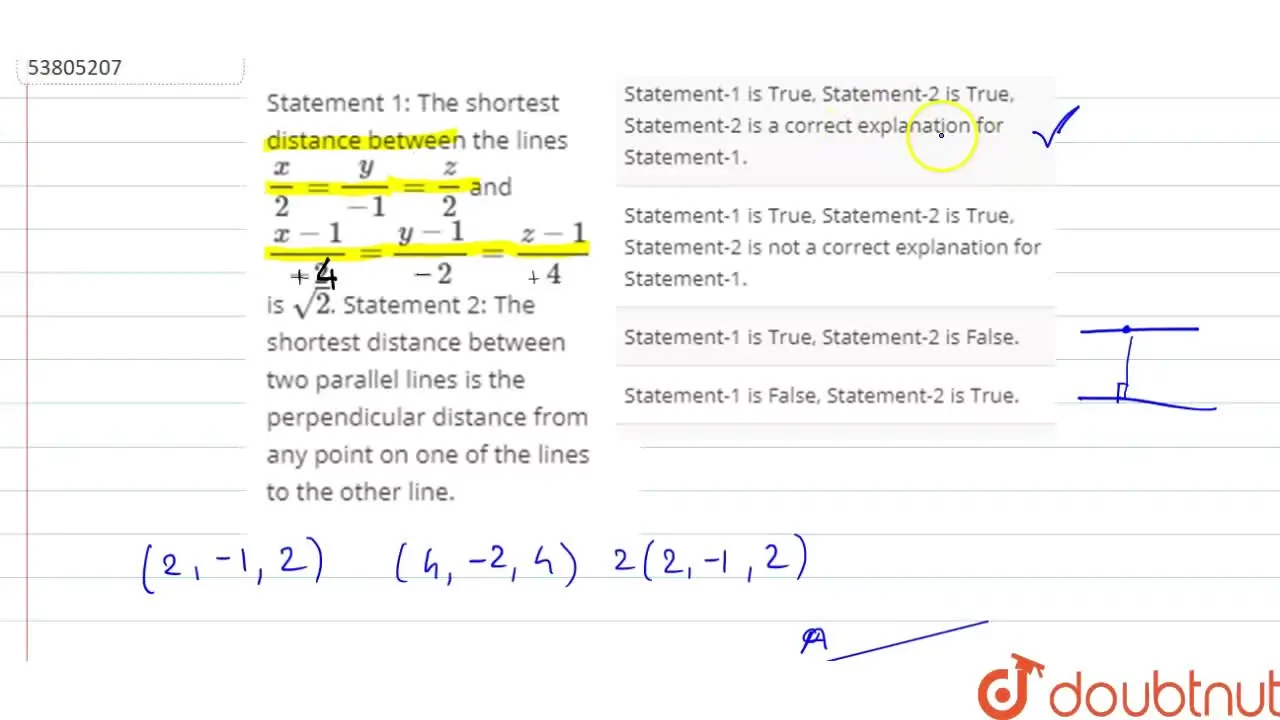
Statement 1: The shortest distance between the lines $\frac{x}{2}=\frac{y}{-1}=\frac{z}{2}$ and $\frac{x-1}{-2}=\frac{y-1}{-2}=\frac{z-1}{4}$ is $\sqrt{2}$. Statement 2: The shortest distance between two parallel lines is the perpendicular distance from any point on one of the lines to the other line.

Options

A. Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1.
B. Statement-1 is True, Statement-2 is True, Statement-2 is not a correct explanation for Statement-1.
C. Statement-1 is True, Statement-2 is False.
D. Statement-1 is False, Statement-2 is True.

Answer

A

Explanation

Clearly, statement -2 is true.
Line `x/2=y/(-1)=z/2` passes through the origin and the line`(x-1)/4=(y-1)/(-2)=(z-1)/4` passes through `A(1,1,1)` and is parallel to the vector `vecb=4hati-2hatj+4hatk`.
Clearly `AL=` Projection of `OA` on `vecb`
`impliesAL=(|vec(OA).vecb|)/(|vecb|)=(|4-2+4|)/(sqrt(16+4+16))=1`
`:.OL=sqrt(|vec(OA)|^(2)-AL^(2))`
`impliesOL=sqrt(3-1)=sqrt(2)vecb=4hati-2hatj+4hatk`
Hence statement -1 is true and statement -2 is a correct explanation of statement -1.