Let A and B be two events such that p(¯¯¯A∪B)=16,p(A∩B)=14 and p(¯¯¯A)=14 , where ¯¯¯A stands for the complement of the event A. Then the events A and B are (1) mutually exclusive and independent (2) equally likely but not independent (3) independent but not equally likely (4) independent and equally likely
mutually exclusive and independent
independent but not equally likely
equally likely but not independent
equally likely and mutually exclusive
The correct Answer is:B
We have, P(A∪B)=14≠0
So, A and B are not mutually exclusive events.
Now,
P(¯¯¯¯¯¯¯¯¯¯A∪B)=16
⇒1−P(A∪B)=16
⇒P(A∪B)=56
⇒P(A)+P(B)−P(A∩B)=56
⇒34+P(B)−14=56⇒P(B)=13
Clearly, P(A∪B)=14=34×13=P(A)P(B)
So, A and B are independent.
Also, P(A)≠P(B). So, A and B are not equally likely.
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Section I - Solved Mcqs126videos
PROBABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Section- II (Assertion -Reason Types MCQs)15videos
PROBABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Chapter Test60videos
PERMUTATIONS AND COMBINATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - QUADRATIC EXPRESSIONS AND EQUATIONS EXERCISE - Chapter Test50videos
QUADRATIC EXPRESSIONS AND EQUATIONS
Similar Questions
Let A and B be two events such that P¯¯¯¯¯¯¯¯¯¯¯¯¯(A∪B)=16,P(A∩B)=14andP(¯¯¯A)=14 where ¯¯¯A stands for complement of event A. Then, events A and B are
View SolutionLet A and B be two events such that
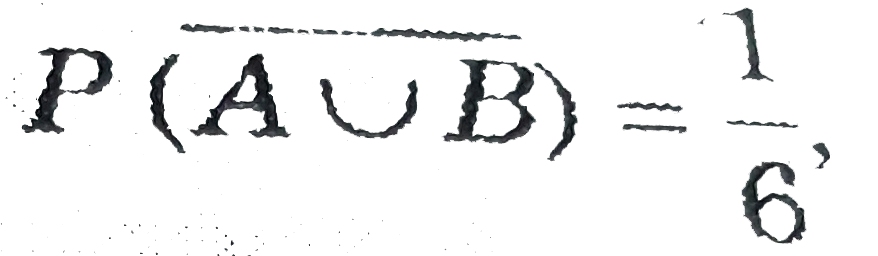 ,P(A cap B)=(1)/(4)andPoverset(-)(A)=(1)/(4),whereoverset(-)A stands for the complement of the event A. Then, the events A and B are View Solution
,P(A cap B)=(1)/(4)andPoverset(-)(A)=(1)/(4),whereoverset(-)A stands for the complement of the event A. Then, the events A and B are View Solution
Knowledge Check
- Question 1 - Select One
Let A and B be two events such that P(¯¯¯¯¯¯¯¯¯¯A∪B)=16,P(A∩B)=14andP(¯¯¯A)=14,where¯¯¯A stands for the complement of the event A. Then the events A and B are
Amutually exclusive and independentBequally likely but not independentCIndependent but not equally likelyDindependent and equally likely - Question 2 - Select One
Let A and B be two events such that P(¯¯¯¯¯¯¯¯¯¯A∪B)=16,P(A∩B)=14andP(¯¯¯A)=14,where¯¯¯A stands for the complement of the event A. Then the events A and B are
Amutually exclusive and independentBequally likely but not independentCindependent but not equally likelyDindependent and equally likely - Question 3 - Select One
If A and B are any two events such that P(A∪B)=34,
P(A∩B)=14andP(¯¯¯A)=23, where ¯¯¯A stands for the complementary event of A, then what is P(B) ?A13B23C19D29
Let A and B be two events such that P¯¯¯¯¯¯¯¯¯¯¯¯¯(A∪B)=16,P(A∩B)=14andP(¯¯¯A)=14,where ¯¯¯A stands for complement of event A. then , events A and B are
View SolutionLet A and B be events such that P(¯¯¯A)=45,P(B)=13,P(AB)=16 then
View SolutionLet A and B be independent events such that P(A) =0.6 and P(B ) =0.4.
find P(A∩B)View SolutionLet A and B be independent events such that P(A) =0.6 and P(B ) =0.4.
find P(A∩B)View SolutionLet A and B be independent events such that P(A) =0.6 and P(B ) =0.4.
find P(A∩¯¯¯B)View Solution

