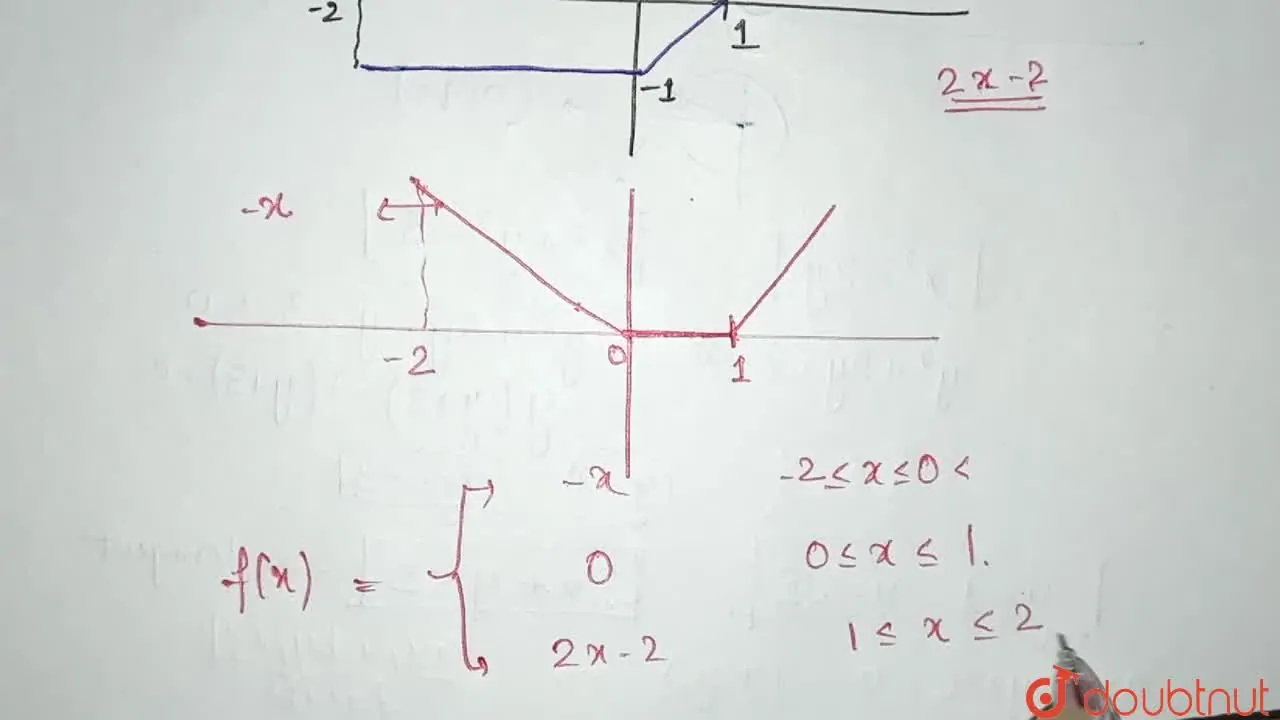
Let f(x) be defined on [-2,2] and is given by
f(x)={−1−2≤x≤0x−10<x≤2
and g(x)=f(|x|)+|f(x)|. Then g(x) is equal to
⎧⎪⎨⎪⎩−x−2≤x<000≤x<1x−11≤x≤2
⎧⎪⎨⎪⎩−x−2≤x<000≤x<12(x−1)1≤x≤2
{−x−2≤x<0x−10≤x≤2
none of these
The correct Answer is:B
Step by step video, text & image solution for Let f(x) be defined on [-2,2] and is given by f(x)={{:(,-1,-2 le x le 0),(,x-1,0 lt x le 2):} and g(x)=f(|x|)+|f(x)|. Then g(x) is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - FUNCTIONSEXERCISE - Chapter Test30videos
FUNCTIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - FUNCTIONSEXERCISE - Section II - Assertion Reason Type10videos
FUNCTIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Exercise40videos
DISCRETE PROBABILITY DISTRIBUTIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - HYPERBOLAEXERCISE - Chapter Test29videos
HYPERBOLA
Similar Questions
Let f(x) be defined on [−2,2] and be given by
f(x)={−1,−2≤x≤0x−1,0<x≤2andg(x)=f(|x|)+|f(x)|.
Then find g(x).View SolutionLet f(x) be defined on [-2,2[ such that f(x)={−1−2≤x≤0x−10≤x≤2 and g(x)=f(|x|)+|f(x)|. Then g(x) is differentiable in the interval.
View SolutionLet f(x) be defined on [-2,2] and is given by
f(x) = {x+1−2≤x≤0x−10≤x≤2, then f (|x|) is defined asView SolutionLet f(x)={−1−2≤x<0x2−10≤x≤2 and g(x)=|f(x)|+f(|x|). Then , in the interval (-2,2),g is
View SolutionLet f(x)={−1,−2≤x<0x2−1,0≤x≤2 and g(x)=|f(x)|+f(|x|). Then in the interval (−2,2), g is
View SolutionIf f(x)={x2+10≤x<1−3x+51≤x≤2
View SolutionLet f(x)={1+x,0≤x≤23−x,2<x≤3
find (fof) (x).View SolutionIf f(x)={1+x0≤x≤23x−22<x≤3, then f(f(x)) is not differentiable at:
View SolutionLet f(x) and g(x) be two functions given by f(x)=−1|x−1|,−1≤x≤3 and g(x)=2−|x+1|,−2≤x≤2
Then,View SolutionLet f(x)={2−x,−3≤x≤0x−2,0<x<4 Then f−1 (x) is discontinous at x=
View Solution