In how many ways can 30 marks be allotted to 8 question if each question carries at least 2 marks?
21C7
21C8
21C9
none of these
The correct Answer is:A
Let x1 denote the marks assigned to the ith question. Then,
x1+x2+x3+x4+x5+x6+x7+x8=30
where x1≥2,i=1,2,....,8.
Let, yi=xi−2,i=1,2,....8. Then,
x1+x2+x3+....x8=30
⇒y1+y2+y3+......+y8=14
The total number of solutions of this equation is
14+8−1C8−1=21C7.
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Section II - Assertion Reason Type
9 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Exercise
136 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Chapter Test
60 Videos
- PARABOLABOOK - OBJECTIVE RD SHARMACHAPTER - PARABOLAEXERCISE - Chapter Test
30 Videos
- PROBABILITY BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Chapter Test
45 Videos
Similar Questions
Knowledge Check
In how many ways can 8 different books be distributed among 3 students if each receives at least 2 books ?
A[8!(2!)24!2!+8!2!2!]B[8!(2!)24!2!+8!2!2!]×3!C[8!(2!)24!2!]×3!D[8!(2!)24!+8!(3!)22!]×3!There are 10 questions in a question paper. In how many ways, a student can solve these questions, if he solves one or more questions?
A1024B1025C1023D1000There are three section A,B, C in a paper each section having 5 questions . In how many ways a student can solve exactly 5 questions taken at least one question from each section.
A2200B2225C2250D2275
In how many ways a student can attempt 6 questions from an examination paper consisting 8 questions?
View SolutionIn an exam, there were 50 questions and each question carries 4 marks. Sahil scored 80% marks in the test. Later 5 questions were proved logically incorrect and the score of each student was calculated out of the rest of the questions. What is Sahil's new score, if he hadn't answered any of the deleted questions?
View SolutionIn an exam, there were 50 questions and each question carries 4 marks. Sahil scored 80% marks in the test. Later 5 questions were proved logically incorrect and the score of each student was calculated out of the rest of the questions. What is Sahil's new score, if he hadn't answered any of the deleted questions?
View SolutionDirections: In a Mathematics exam of 50 marks, there are five questions of 1 mark each, fifteen questions 2 mark each and 3 questions of 5 mark each. Given below is a table that shows number of correct answers of some students in different categories and then total marks out of 50. Some fields have been left as empty and then respective values needs to be calculated if the need arises. Based on this information, answer the questions that follow.
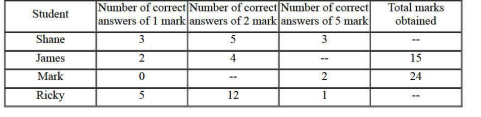
How many questions of 2 marks have been answered correctly by James and Mark together?
View SolutionAnswer the following questions independently of each other
In how many ways can 12 identical bouquets be kept in 3 distinct crates so that at least 2 bouquets must be there in each bouquet ?
View Solution
