A rectangle with sides of lengths (2n−1)and(2m−1) units is divided into squares of unit length. The number of rectangles which can be formed with sides of odd length, is
m2n2
mn(m+1)(n+1)
4m+n−1
none of these
The correct Answer is:A
Clearly,
Number of horizontal rectangles of 1 units length =(2m−1)
Number of horizontal rectangles of 3 unit length =(2m−3)
Number of horizontal rectangles of 5 unit length =(2m−5)
Similarly,
Number of rectangles of (2m−1) unit length =1
∴ Total number of horizontal rectangles of odd length
=(2m−1)+(2m−3)+....+3+1=m2
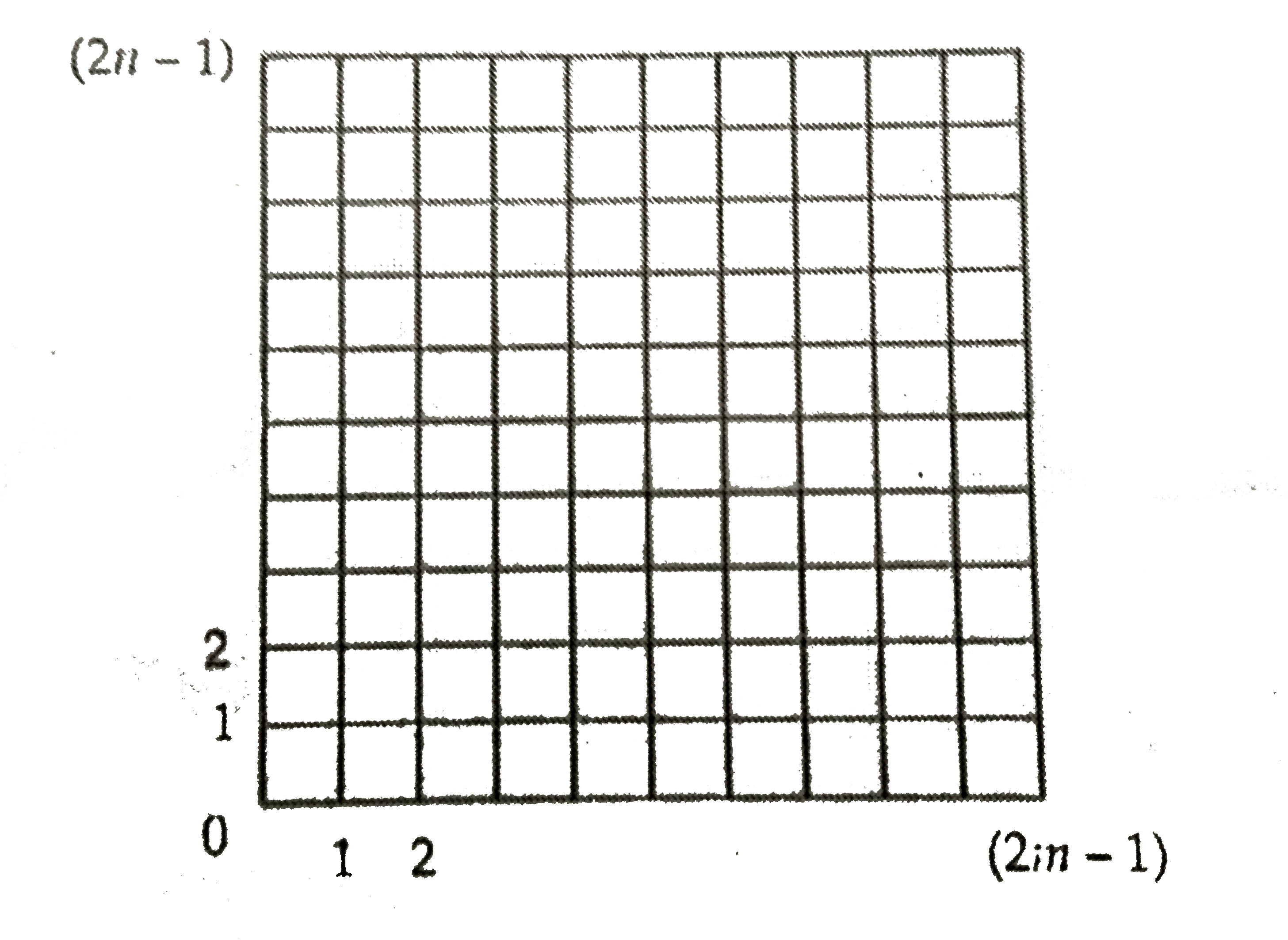
Similarly
Total number vertical rectangles of odd length =n2
∴ Total numbr of rectangles =m2×n2
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Section I - Solved Mcqs
111 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Section II - Assertion Reason Type
9 Videos
- PARABOLABOOK - OBJECTIVE RD SHARMACHAPTER - PARABOLAEXERCISE - Chapter Test
30 Videos
- PROBABILITY BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Chapter Test
45 Videos
Similar Questions
A rectangle with sides of lengths 15 and 13 unitsis divided into squares of sides of unit length. Thennumber of rectangles which can be formed with thesides of odd length, is
View SolutionThere is a rectangular sheet of dimension (2m−1)×(2n−1), (where m>0,n>0) It has been divided into square of unit area by drawing line perpendicular to the sides. Find the number of rectangles having sides of odd unit length.
View Solution
Knowledge Check
A rectangle with sides of lengths (2n−1)and(2m−1) units is divided into squares of unit length. The number of rectangles which can be formed with sides of odd length, is (a) m2n2 (b) mn(m+1)(n+1) (c) 4m+n−1 (d) non of these
A(m+n+1)2B4(m+n−1)Cm2n2Dmn(m+1)(n+1)There is a rectangular sheet of dimensions (2m−1)×(2n−1) (where m>0,n>0) It has been divided into squares of unit area by drawing lines perpendicular to the sides. Find number of rectangles having sides of odd unit length.
A(m+n+1)2Bmn(m+1)(n+1)C4m+n−2Dm2n2The length of rectangle is (7x - 3y) units and its breadth is (3x + 4y) units. The perimeter of the rectangle is
A(13x + 5y) unitsB(17x - 2y) unitsC(20x + 2y) unitsD(10x + y) units
find the length of the diagonal of a rectangle whose sides are 8 m and 6m.
View SolutionThe area of a square of one side 8 cm is equal to the area of a rectangle. Which of the following statements about the rectangle is/are correct?
(1) The length of the rectangle is 16 times of the breadth
(2)The length of the rectangle is 32 times of the breadth
(3) The breadth of the rectangle is 16 of the length
(4) The breadth of the rectangle is 19 is the length
View SolutionLet each side of smallest square of chess boards is one unit in length. Find the total number of rectangles (including squares) whose side parallel to side of chess board
View SolutionA wire of length 20m is to be folded in the form of a rectangle. How many rectangles can be formed by folding the wire if the sides are positive integers in metres?
View SolutionThe length of the diagonal of a rectangle with sides 4 m and 3m would be
View Solution
