If l1,m1,n1,l2,m2,n2andl3,m3,n3 are direction cosines of three mutuallyy perpendicular lines then, the value of ∣∣ ∣∣l1m1n1l2m2n2l3m3n3∣∣ ∣∣ is
l3m3n3
±1
l1m1n1
l2m2n2
The correct Answer is:B
Since, l1,m1,n1,l2,m2,n2andl3,m3,n3 are direction cosines of three mutually perpendicular lines
∴l21+m21+n21−1,l22+m22+n22=1
l23+m23+n23=1,l1l2+m1m2+n1n2=0
l1l3+m1m3+n1n3=0,l2l3+m2m3+n2n3=0
Let Δ=∣∣
∣∣l1m1n1l2m2n2l3m3n3∣∣
∣∣. Then,
Δ2=∣∣
∣∣l1m1n1l2m2n2l3m3n3∣∣
∣∣∣∣
∣∣l1m1n1l2m2n3l3m3n3∣∣
∣∣
=∣∣
∣
∣∣l21+m21+n21l1l2+m1m2+n1n2l1l3+m1m3+n1n3l1l2+m1m2+n1n2l21+m22+n22l2l3+m2m3+n2n3l1l3+m1m3+n1n3l1l3+m2m3+n2n3l23+m23+n23∣∣
∣
∣∣
=∣∣
∣∣100010001∣∣
∣∣=1
∴Δ=±1
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMACHAPTER - DETERMINANTSEXERCISE - Section I - Solved Mcqs74videos
DETERMINANTS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DETERMINANTSEXERCISE - Section II - Assertion Reason Type6videos
DETERMINANTS
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONIC SECTIONSEXERCISE - Section I - Solved Mcqs1videos
CONIC SECTIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Exercise40videos
DISCRETE PROBABILITY DISTRIBUTIONS
Similar Questions
Let li,mi,ni;i=1,2,3 be the direction cosines of three mutually perpendicular lines referred to an orthogonal cartesian co–ordinate system, then prove that A=⎡⎢⎣l1m1n1l2m2n2l3m3n3⎤⎥⎦is an orthogonal matrix.
View SolutionThree concurrent lines with direction cosines (l1,m1,n1),(l2,m2,n2)and(l3,m3,n3) are coplanar if
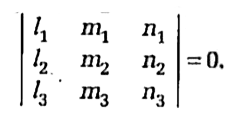 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A=⎡⎢⎣l1m1n1l2m2n2l3m3n3⎤⎥⎦ and B=⎡⎢⎣p1q1r1p2q2r2p3q3r3⎤⎥⎦
Where pi,qi,ri are the co-factors of the elements li,mi,ni for i=1,2,3. If (l1,m1,n1),(l2,m2,n2) and (l3,m3,n3) are the direction cosines of three mutually perpendicular lines then (p1,q1,r1),(p2,q2,r2) and (p3,q,r3) areAthe direction cosines of three mutually perpendicular linesBthe direction ratios of three mutually perpendicular lines which are not direction cosines.Cthe direction cosines of three lines which need not be perpendicularDthe direction of three lines which need not be perpendicular - Question 2 - Select One
(l1,m1,n1),(l2,m2,n2),(l3,m3,n3) are the direction cosines of three mutually perpendicular lines. If the line, whose direction ratios are l1+l2+l3,m1+m2+m3,n1+n2+n3, makes angle θ with any of these three lines, then cosθ is equal to
A12B13C1√3Dnone of these - Question 3 - Select One
The direction cosines of a line equally inclines to three mutually perpendicular lines having D.C.'s
as (l1,m1,n1),(l2,m2,n2),(l3,m3,n3) areAthe direction cosines of three mutually perpendicular linesBthe direction ratios of three mutually perpendicular lines which are not direction cosines.Cthe direction cosines of three lines which need not be perpendicularDthe direction of three lines which need not be perpendicular
The three lines through the origin with direction cosines l1,m1,n1,l2,m2,n2, and l3,m3,n3 are coplanar, if
View SolutionLet l1,m1,n1;l2,m2,n2 and l3,m3,n3 be the direction cosines of three mutually perpendicular lines. Show that the direction ratios of the line which makes equal angles with each of them are (l1+l2+l3),(m1+m2+m3),(n1+n2+n3)
View SolutionIf l1,m1,n1 and l2,m2,n2 are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are m1n2−m2n1,n1l2−n2l1,l1m2−l2m1.
View SolutionLet l1,m1,n1,l2,m2,n2 and l3,m3,n3 are direction cosine of three mutually perpendicular line OA, OB and OC. If the direction cosines of OP are proportional to l1+l2+l3,m1+m2+m3,n1+n2+n3 and angle made by OP with lines OA, OB, OC are respectively θ1,θ2,θ3, then
View SolutionThe direction cosines of a line equally inclined to three mutually perpendiclar lines having direction cosines as l1,m1,n1,l2,m2,n2 and l3,m3,n3 are
View Solution

