Find the values of $θ$ in the interval $(- \frac{π}{2}, \frac{π}{2})$ satisfying the equation $(1 - tan θ) (1 + tan θ) {sec}^{2} θ + 2^{tan}^(2 θ) = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $θ = \pm π / 3$

Given, $(1 - tan θ) (1 + tan θ) {sec}^{2} θ + 2^{{tan}^{2} θ} = 0$
$\Rightarrow (1 - {tan}^{2} θ) \cdot (1 + {tan}^{2} θ) + 2^{{tan}^{2} θ} = 0$
$\Rightarrow 1 - {tan}^{4} θ + 2^{{tan}^{2} θ = 0}$
Put ${tan}^{2} θ = x$
$∴ 1 - x^{2} + 2^{x} = 0$
$\Rightarrow x^{2} - 1 = 2^{x}$ .
Note $2^{x} and x^{2} - 1$ are uncompatible functions, therefore we have to consider range to both functions.
Curve $y = x^{2} - 1 and y = 2^{x}$

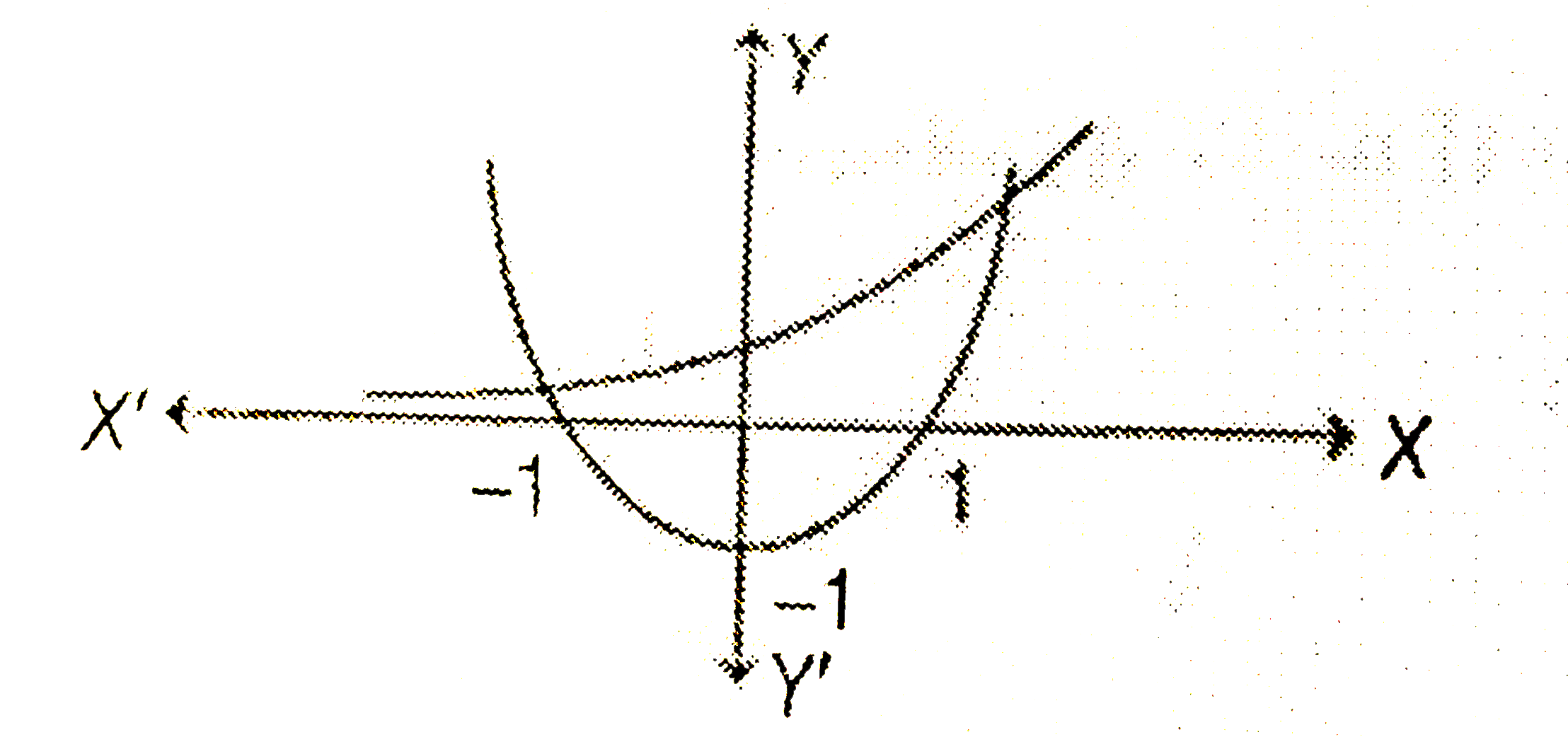
It is clear from the graph that two curves intersect at one point at $x = 3, y = 8$ .
Therefore, ${tan}^{2} θ = 3$ .
$\Rightarrow tan θ = \pm \sqrt{3}$ .
$\Rightarrow θ = \pm \frac{π}{3}$

Updated on:21/07/2023

|

Class 12 MATHS TRIGONOMETRICAL EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The number of values of $θ$ in the interval $[- π, π]$ satisfying the equation $cos θ + sin 2 θ = 0$ is
A1
B2
C3
D4
The possible value of $θ \in [- π, π]$ satisfying the equation $2 (cos θ + cos 2 θ) + (1 + 2 cos θ) sin 2 θ = 2 sin θ$ are
A $- \frac{π}{2}$
B $- \frac{π}{3}$
C $\frac{π}{3}$
D $π$

IIT JEE PREVIOUS YEAR-TRIGONOMETRICAL EQUATIONS-ANALYTICAL & DESCRIPTIVE QUESTIONS

Home
Ask Doubt
Profile