A vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring , so that the spring is compressed by a distance d. The net work done in the process is
mg(h+d)−12kd2
mg(h−d)−12kd2
mg(h−d)+12kd2
mg(h+d)+12kd2.
The correct Answer is:A
When a mass falls on a spring from a height h the work done by the loss of potential energy of the mass is stored as the potential energy of the spring.
One can write from conservation of energy that, mg(h+d)=12kd2

mg(h+d)=12kx2=12kd2
The two energies are equal.
If work done is initial P.E. - final P.E., it is zero.
Work done is totally converted (assuming there is no loss). The work done in compression or expansion is always positive as it is directly proportional to x2. The answer expected is mg(h+d)−12kd2 or, 12kd2−mg(h+d) as seen from options, but it is not justified. Question could have been more specific like work done by oscillation.
Topper's Solved these Questions
- WORK, POWER, ENERGYBOOK - MTG-WBJEECHAPTER - WORK, POWER, ENERGYEXERCISE - EXERCISE (WB JEE WORKOUT) CATEGORY 3 : One or More than One Option Correct Type (2 Marks)
10 Videos
- WORK, POWER, ENERGYBOOK - MTG-WBJEECHAPTER - WORK, POWER, ENERGYEXERCISE - EXERCISE (WB JEE Previous Years Questions) CATEGORY 1 : Single Option Correct Type (1 Mark)
3 Videos
- WORK, POWER, ENERGYBOOK - MTG-WBJEECHAPTER - WORK, POWER, ENERGYEXERCISE - EXERCISE (WB JEE Previous Years Questions) CATEGORY 1 : Single Option Correct Type (1 Mark)
3 Videos
- WAVE OPTICSBOOK - MTG-WBJEECHAPTER - WAVE OPTICSEXERCISE - WB JEE PREVIOUS YEARS QUESTION (MCQ.s)
9 Videos
Similar Questions
A ball of mass m is droppped from a height h on a platform fixed at the top of a vertical spring. The platform is depressed by a distance x. What is the spring constant K?
View SolutionFigure. shows a rough horizontal plane which ends in a vertical wall, to which a spring is connected, having a force constant k. Initially spring is in its relaxed state. A block of mass m starts with an initial velocity u towards the spring from a distance l0 from the end of spring shown. When block strikes at the end ofthe spring, it compresses the spring and comes to rest. Find the maximum compression in the spring. The friction coefficient between the block and the floor is μ..
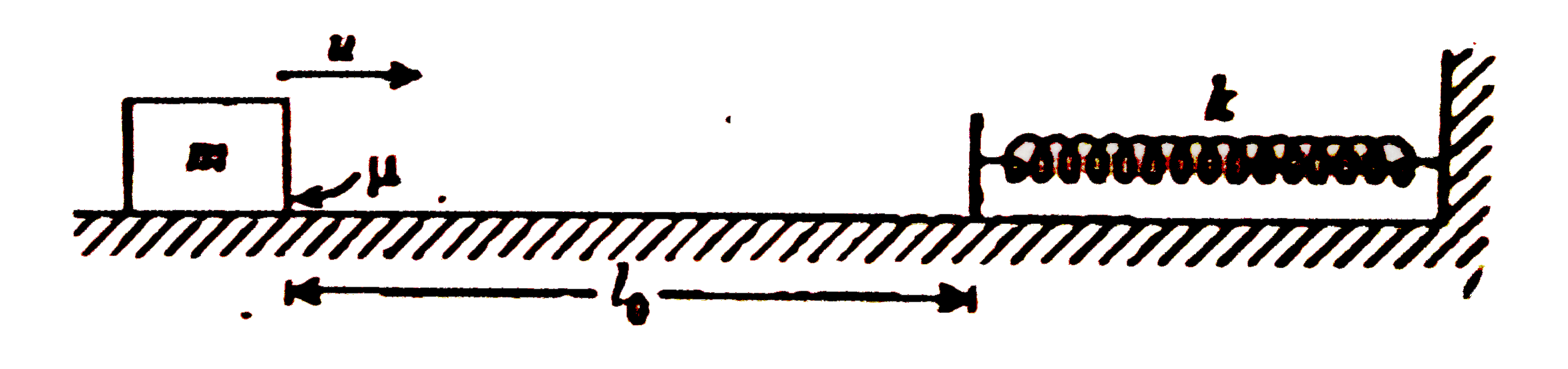
View Solution
Knowledge Check
A ball of mass m is dropped from a heighth on a platform fixed at the top of a vertical spring, as shown in figure. The platform is depressed by a distance x. Then the spring constant is
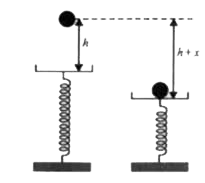 Amg(h+x)Bmg(h+2x)C2mg(h+x)x2Dmg(2h+x)
Amg(h+x)Bmg(h+2x)C2mg(h+x)x2Dmg(2h+x)A massless spring of length l and spring constant k is placed vertically on a table. A ball of mass m is just kept on top of the spring. The maximum velocity of the ball is
Ag√mkBg√2mkCg2√mkDg√m2kA spring of force constant K rests on a smooth floor, with one end fixed to a wall. A block of mass m hits the free end of the spring with velocity v. The maximum force exerted by the spring on the wall is
Av√(mk)Bmv√kCm√(vk)Dk√(mv)
A spring is compressed by 10 cm by a ball of mass 20 g . What will be the potential energy of a spring if the force constant of the spring is 20 N cm−1 .
View SolutionA spring of force constant 600Nm−1 is mounted on a horizontal table. A mass of 1.5 kg is attached to the free end of the spring,pulled sideways to a distance of 2 cm and released . The speed of the mass when the spring is compressed by 1 cm is
View SolutionOne end of a spring of force constant k is fixed to a vertical wall and the other to a blcok of mass m resting on a smooth horizontal surface. There is another wall at distance x0 from the block. The spring is then compressed by 2x0 and released. The time taken to strike the wall is

View SolutionA force of 10 N holds an ideal spring with a 20Nm spring constant in compression. The potential energy stored in the spring is
View SolutionA slab S of mass m released from a height h0, from the top of a spring of force constant k. The maximum compression x of the spring is given by the equation.
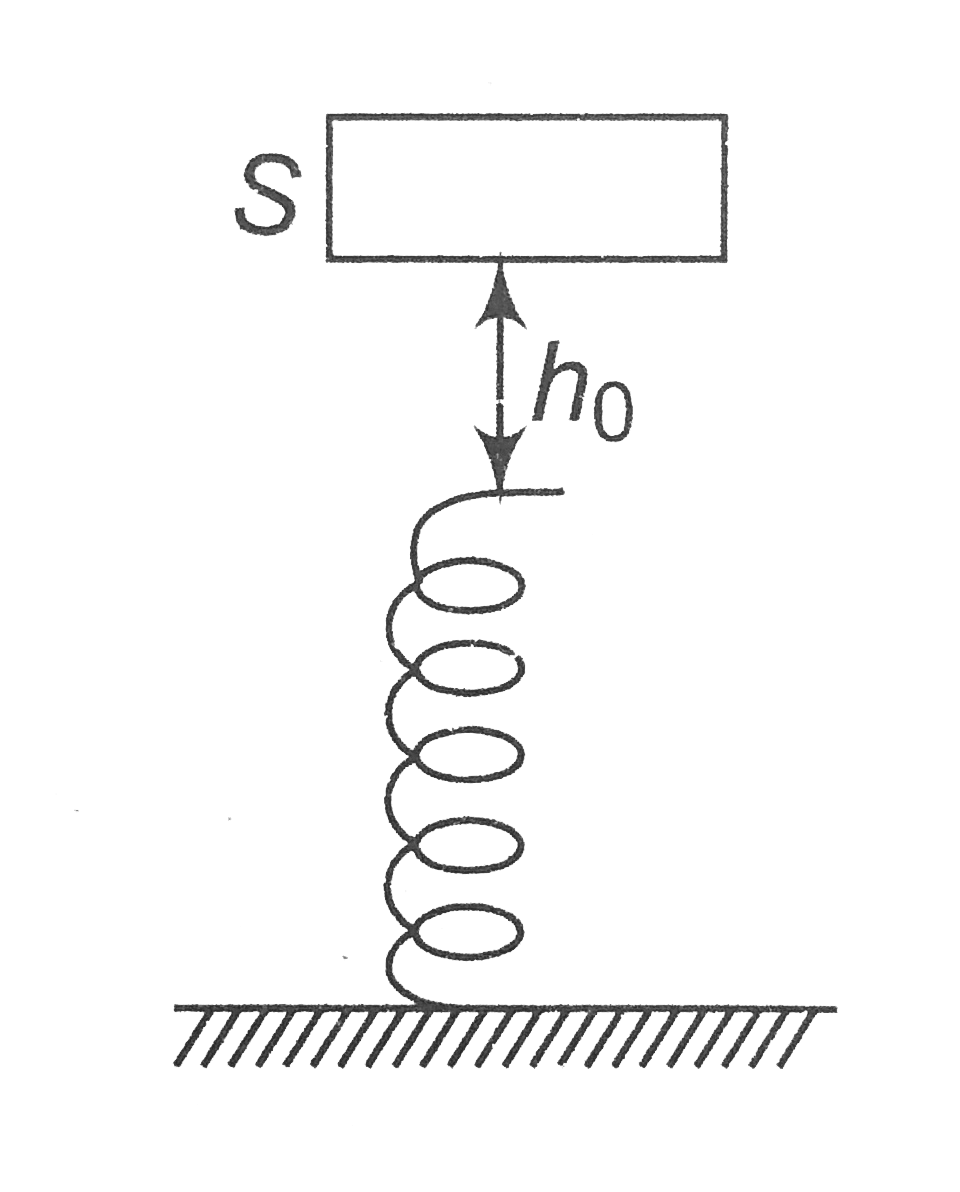
View Solution
