A force F=Kx2 acts on a particle at an angle of 60° with the x–axis. the work done in displacing the particle from x1 to x2 will be –
k6(x22−x21)
k6(x32−x31)
k(x2−x1)
k(x32−x31).
The correct Answer is:B
We know work done =dW=→F.d→x=Fdxcosθ
∴W=∫x2x1F.dx.cos60∘=12[∫x2x1kx2.dx]
⇒W=k2∫x2x1x2dx=k2[x33]x2x1=k6(x32−x31).
Topper's Solved these Questions
- WORK, POWER, ENERGYBOOK - MTG-WBJEECHAPTER - WORK, POWER, ENERGYEXERCISE - EXERCISE (WB JEE WORKOUT) CATEGORY 2 : Single Option Correct Type (2 Mark)
15 Videos
- WORK, POWER, ENERGYBOOK - MTG-WBJEECHAPTER - WORK, POWER, ENERGYEXERCISE - EXERCISE (WB JEE WORKOUT) CATEGORY 3 : One or More than One Option Correct Type (2 Marks)
10 Videos
- WAVE OPTICSBOOK - MTG-WBJEECHAPTER - WAVE OPTICSEXERCISE - WB JEE PREVIOUS YEARS QUESTION (MCQ.s)
9 Videos
Similar Questions
A force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View SolutionIf force F=(2x+3x2)N is applied on a particle along x = axis, then find the work done by it during motion of particle from x = 0 to x = 2 m.
View Solution
Knowledge Check
A force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
A−k2aB−kaC−2kaD−akA force F acting on a particle varies with the position x as shown in the graph. Find the work done by the force in displacing the particle from x=−a to x=+2a.
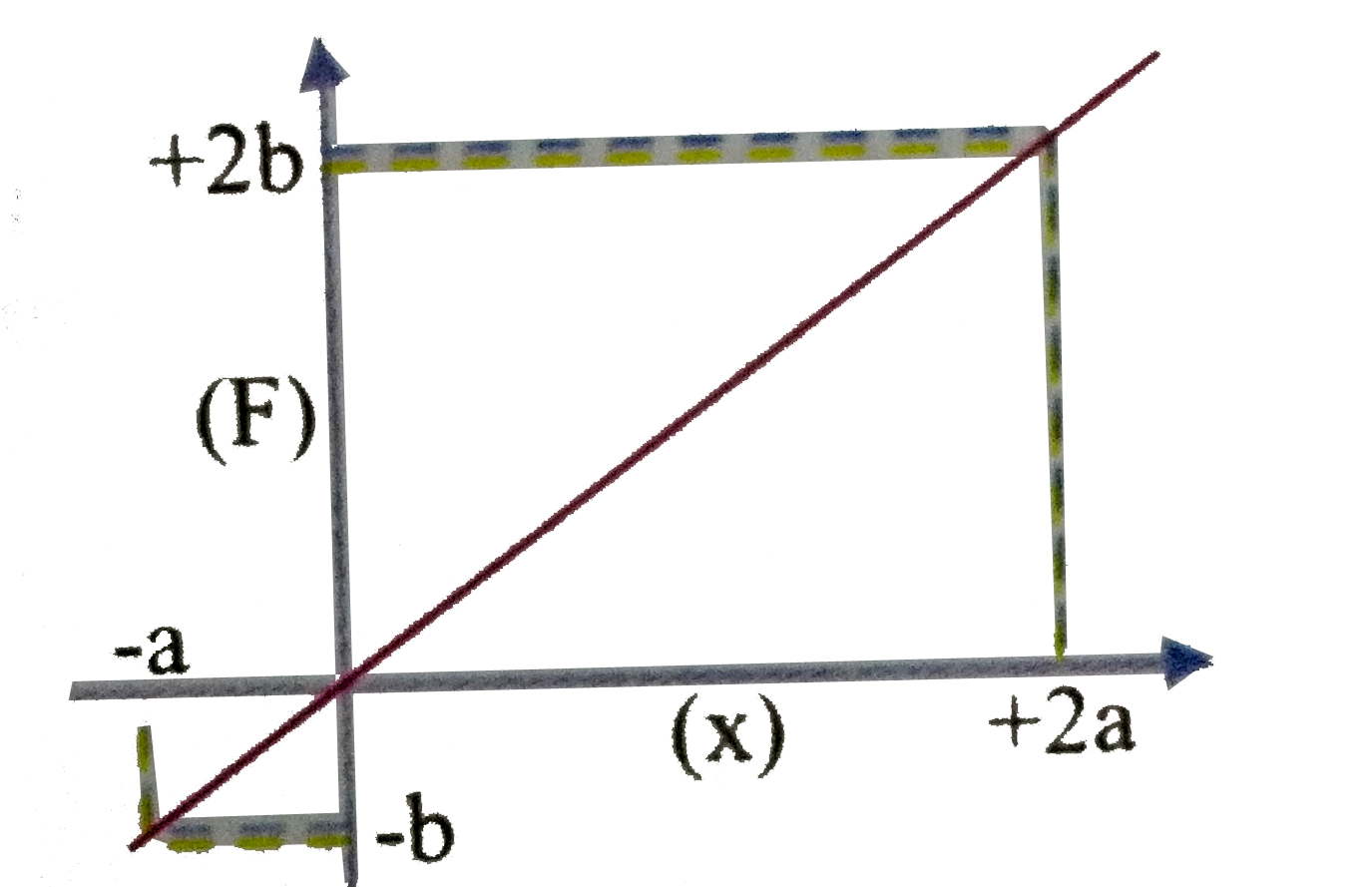 .A3ab2B4ab2C23abD24ab
.A3ab2B4ab2C23abD24abA force of F=(0.5x+12)N acts on a particle. If x is in metre, calculate the work done by the force during the displacement of the particle from x = 0 to x = 4 m
A128 JB80 JC64 JD52 J
A force F=a+bx acts on a particle in x-direction, where a and b are constants. Find the work done by this force during the displacement from x1 to x2.
View SolutionA force F=(a+bx) acts on a particle in x direction where a and b are constants . Find the work done by this force during displacement from x1 to x2 .
View SolutionA force F = (2+ x)N acts on a particle in the x-direction. The work done by this force during a displacement from x = 1.0 m to x = 2.0 m is
View SolutionA force f=10+2x acts on a particle moving in straight line on x axis the work done by this force during a displacement from x=0 and x=3m
View SolutionThe force acting on a bod moving parallel to the X-axis is F=3x+2x2. What is the work done in displacing the body from x=1 to x=2?
View Solution
