माना →C=→A+→B तब
∣∣→C हमेशा ∣∣→A∣∣ से अधिक है
∣∣→C∣∣<∣∣→A∣∣ तथा ∣∣→C∣∣<∣∣→B∣∣ संभव हो सकता है
C हमेशा A+B के बराबर है
C,A+B के बराबर नहीं हो सकता
The correct Answer is:B
→C=→A+→B
C का मान A-B तथा A+B के मध्य होगा
∣∣→C∣∣<∣∣→A∣∣ अथवा ∣∣→C∣∣<∣∣→B∣∣
Topper's Solved these Questions
- गणितीय अवधाराणाएं एवं सदिशBOOK - ERRORLESS HINDICHAPTER - गणितीय अवधाराणाएं एवं सदिशEXERCISE - Ordinary Thinking ( सदिश गुणन )
36 Videos
- गणितीय अवधाराणाएं एवं सदिशBOOK - ERRORLESS HINDICHAPTER - गणितीय अवधाराणाएं एवं सदिशEXERCISE - Ordinary Thinking ( लामी प्रमेय)
3 Videos
- गणितीय अवधाराणाएं एवं सदिशBOOK - ERRORLESS HINDICHAPTER - गणितीय अवधाराणाएं एवं सदिशEXERCISE - Ordinary Thinking ( सदिश अवधारणा)
27 Videos
- किरण प्रकाशिकीBOOK - ERRORLESS HINDICHAPTER - किरण प्रकाशिकीEXERCISE - Self Evaluation Test (किरण प्रकाशिकी)
26 Videos
- गुरुत्वाकर्षण BOOK - ERRORLESS HINDICHAPTER - गुरुत्वाकर्षण EXERCISE - Self Evalution Test
17 Videos
Similar Questions
यदि एक सदिश 2ˆi+3ˆj+8ˆk दूसरे सदिश 4ˆj−4ˆi+αˆk पर लम्बवत हो तो α का मान होगा
View Solutionतीन समतलीय सदिश P,Q तथा R किसी बिंदु पर कार्यरत है तथा सामयवस्था में है। दिया है P=1.9318 किग्रा भार sinθ1=0.9659 तो R का मान (किग्रा. भार में) है
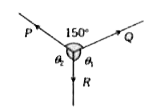
View Solutionसदिश 3ˆi+4ˆk का y- अक्ष पर प्रक्षेप होगा
View Solutionएक खगोलीय दूरदर्शी में सामान्य संजन की स्थिति में, अभिदृश्यक पर एक L लम्बाई की सीधी काली रेखा खींची गई है | नेत्रिका इस रेखा का वास्तविक प्रतिबिम्ब बनाता है | प्रतिबिम्ब की लम्बाई l है | तब दूरदर्शी की आवर्धन क्षमता है
View Solutionपृथ्वी की सूर्य के चारों ओर परिक्रमण कक्ष की माध्य त्रिज्या 1.5×1011 मीटर है। बुध की सूर्य के चारों ओर परिक्रमण कक्ष की माध्य त्रिज्या 6×1010 मीटर है। बुध सूर्य का चक्कर लगाएगा
View SolutionIf →A=→b×→c[→b→c→c],→B=→c×→a[→c→a→b),→C=→a×→b[→a→b→c) find [→A→B→C]
View SolutionIf →a,→band→c are three vectors such that →a×→b=→c,→b×→c=→a,→c×→a=→b then prove that |→a|=∣∣→b∣∣=|→c|
View SolutionLet →a,→band→care vectors such that |→a|=3,∣∣→b∣∣=4and|→c|=5,and(→a+→b) is perpendicular to →c,(→b+→c) is perpendiculatr to →a and (→c+→a) is perpendicular to →b. Then find the value of ∣∣→a+→b+→c∣∣.
View SolutionIf →a,→band→c are three vectors such that →a×→b=→c,→b×→c=→a,→c×→a=→b then prove that |→a|=∣∣→b∣∣=|→c|
View SolutionLet →a,→b,→c be three vectors such that
→a⊥(→b+→c),→b⊥(→c+→a)and→c⊥(→a+→b), if |→a|=1,∣∣→b∣∣=2,
|→c|=3, then ∣∣→a+→b+→c∣∣ is,
View Solutionसिद्ध करें कि
(i) [→a+→b →b+→c →c+→a]=2[→a →b →c]
(ii) →a+→b,→b+→c और →c+→a असमतलीय होगें यदि →a,→b,→c तीन असमतलीय सदिश हों ।
View Solutionयदि →a=→b+→c, तब →a.(→b×→c) बराबर है -
View Solutionयदि सदिश →a,→b,→c इस प्रकार है कि [→a→b→c]=4 तब [→a×→b→b×→c→c×→a]=
View Solutionमाना सदिश →a,→b तथा →c के मापक क्रमश: 3,4 और 5 है और →a+→b+→c=0 तब →a.→b+→b.→c+→c.→a का मान होगा
View SolutionIf →a , →b , →c are three vectors, prove that [→a+→c,→a+→b,→a+→b+→c]=−[→a,→b,→c]
View SolutionLet →a,→b,→c be the three vectors such that →a.(→b+→c)+→b.(→c+→a)+→c.(→a+→b)=0and|→a|=1,∣∣→b∣∣=4,|→c|=8, then ∣∣→a+→b+→c∣∣ equals :
View Solution
