Find Q in the addition.
31Q+1Q3 501
8
2
4
6
The correct Answer is:A
To find the value of Q in the addition 31Q+1Q3=501, we will follow these steps:
Step 1: Set up the equation
We start with the equation:
31Q+1Q3=501
Step 2: Break down the addition
We can express the numbers in terms of Q:
- 31Q can be expressed as 310+Q
- 1Q3 can be expressed as 100+10Q+3
Now, substituting these expressions into the equation gives us:
(310+Q)+(100+10Q+3)=501
Step 3: Simplify the equation
Combine like terms:
310+100+3+Q+10Q=501
This simplifies to:
413+11Q=501
Step 4: Isolate Q
Now, we need to isolate Q by subtracting 413 from both sides:
11Q=501−413
Calculating the right side gives:
11Q=88
Step 5: Solve for Q
Now, divide both sides by 11:
Q=8811
Calculating this gives:
Q=8
Step 6: Verify the solution
To ensure our solution is correct, we can substitute Q=8 back into the original numbers:
- 31Q=318
- 1Q3=183
Now, check the addition:
318+183=501
Since this is correct, our solution is verified.
Final Answer:
Q=8
---
We start with the equation:
31Q+1Q3=501
We can express the numbers in terms of Q:
- 31Q can be expressed as 310+Q
- 1Q3 can be expressed as 100+10Q+3
(310+Q)+(100+10Q+3)=501
Combine like terms:
310+100+3+Q+10Q=501
This simplifies to:
413+11Q=501
Now, we need to isolate Q by subtracting 413 from both sides:
11Q=501−413
Calculating the right side gives:
11Q=88
Now, divide both sides by 11:
Q=8811
Calculating this gives:
Q=8
To ensure our solution is correct, we can substitute Q=8 back into the original numbers:
- 31Q=318
- 1Q3=183
318+183=501
Since this is correct, our solution is verified.
Q=8
Topper's Solved these Questions
Similar Questions
Knowledge Check
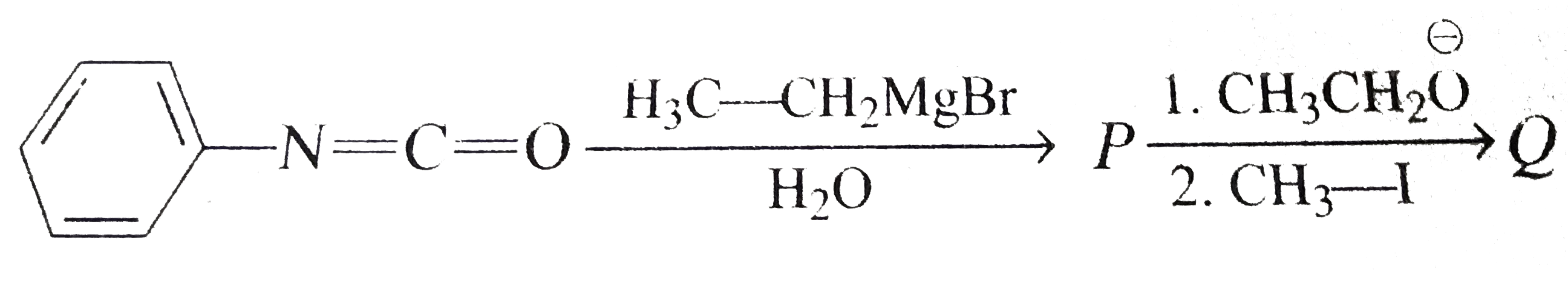 Q
Q
Find out P and Q :APisPh−N=OH∣C−CH2CH3 and Q is O−CH3 ∣Ph−N=C−CH2CH3BPisPh−NH=O∣∣C−CH2CH3 and QisPh−N∣CH3−O∣∣C−CH2CH3CPisPh−NH=O∣∣C−CH2CH3 and QisPh−N=C∣OCH3−CH2CH3DP and Q both are sameFind the mean of the quartiles Q1,Q2 and Q3 of the data 5 , 9 , 8 , 12 , 7 , 13 , 10 , 14.
A9B10C9.5D11.5Let PQR be am acute-angled triangle in which PQ lt QR. From the vertex Q draw altitude Q1, the angle bisector QQ2 and the medianQQ3 With Q1,Q2,Q3 lying on PR. Then
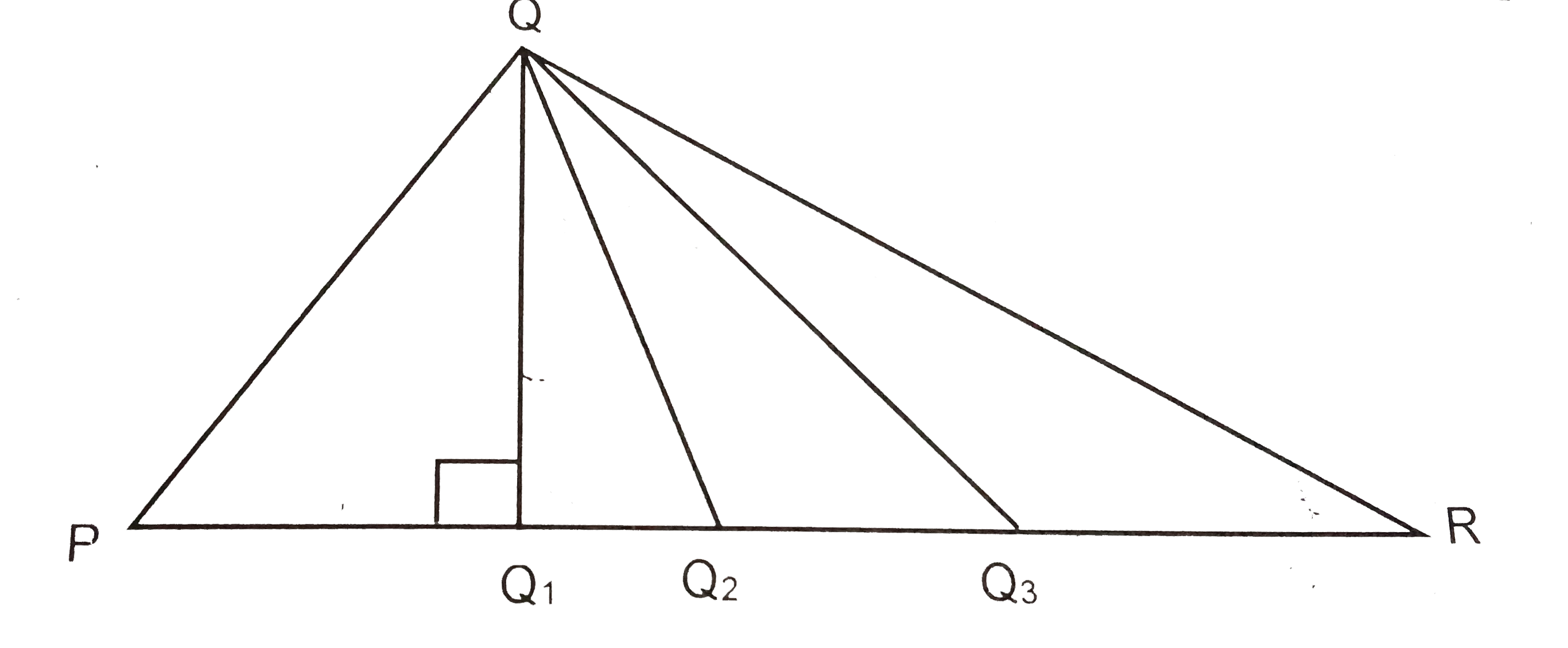 APQ1<PQ2<PQ3BPQ2<PQ1<PQ3CPQ1<PQ3<PQ2DPQ3<PQ1<PQ2
APQ1<PQ2<PQ3BPQ2<PQ1<PQ3CPQ1<PQ3<PQ2DPQ3<PQ1<PQ2
Find k, if PQ ∣∣RS and P(2,4), Q (3,6), R (3,1), S(5,k).
View SolutionAs median divides an arranged series into two equal parts, in similar way quartile divides an arranged series in 4 equal part. For ungrouped frequency distribution formula of finding ith quartile = Q={i.(N+14)}th term, i = 1, 2, 3.term, i = 1, 2, 3. Quartile deviation : half of difference between upper quartile & lower quartile. Quartie deviation (Q.D)=12(Q3−Q1) Coefficient of quartile deviation =(Q3−Q1Q3+Q1). If 1, 2, 3, 4, 5, 6, 7, are numbers then Q1&Q3, are respectively
View SolutionEx-1 Q 31 to 60
View SolutionQ.31 to 38
View SolutionEx-2 Q 31 to 51
View Solution