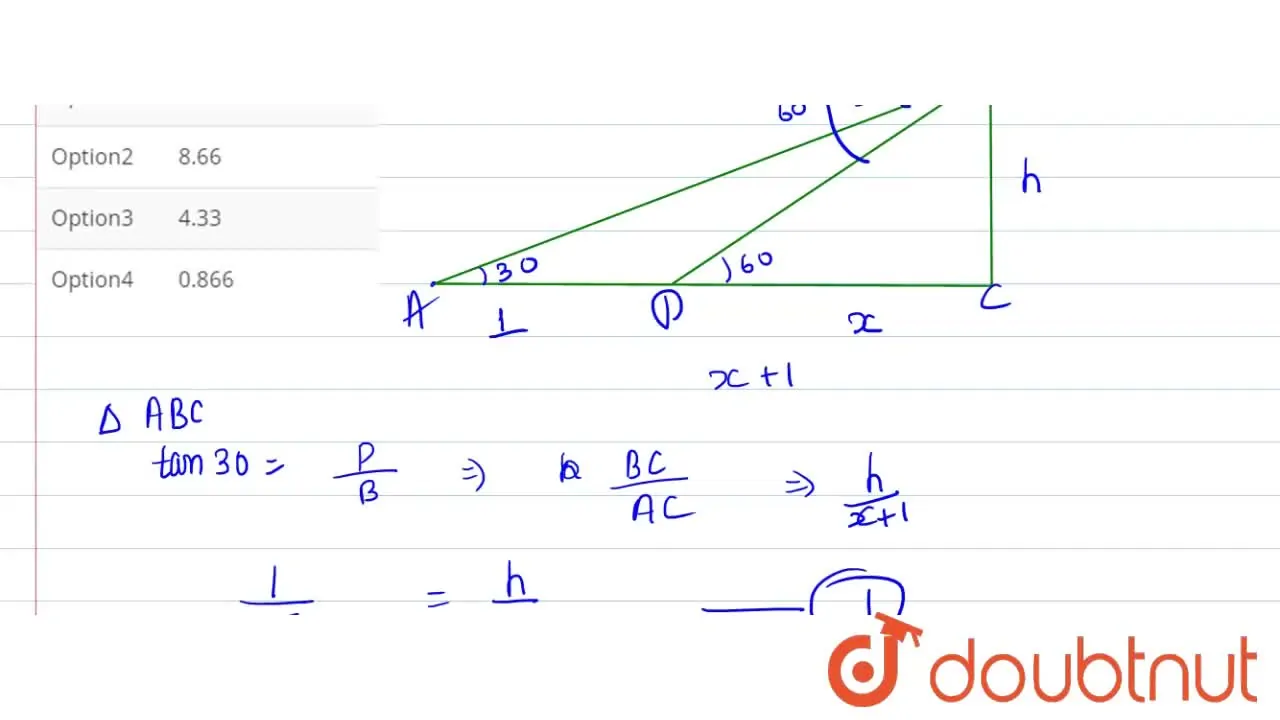
From an aeroplane just over a straight road, the angles of depression of two consecutive kilometre is stones situated at opposite sides of the aeroplane were found to be 60∘ and 30∘ respectively. The height (in km) of the aerophlane from the road at that instant was
(Given √3=1.732)
0.433
8.66
4.33
0.866
The correct Answer is:D
Step by step video, text & image solution for From an aeroplane just over a straight road, the angles of depression of two consecutive kilometre is stones situated at opposite sides of the aeroplane were found to be 60^@ and 30^@ respectively. The height (in km) of the aerophlane from the road at that instant was (Given sqrt(3)= 1.732) by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Similar Questions
From an aeroplane just over a straight road, the angles of depression of two consecutive kilometer stones situated at opposite sides of the aeroplane were found to be 60∘ and 30∘ respectively. The height (in km) of the aeroplene from the road at that instant, is:
एक विमान से ठीक सीधी सड़क पर, विमान की विपरीत दिशाओं में स्थित दो अनुक्रमिक किलोमीटर पत्थरों के अवनमन कोण क्रमशः 60∘ और 30∘ हैं। उस समय विमान की सड़क से ऊँचाई (किमी में) कितनी है?View SolutionFrom an aeroplane vertically over a straight horizontal road, the angles of depression of two consecutive kilometre-stones on the opposite sides of the aeroplane are observed to be αandβ. The height of the aeroplane above the road is
View SolutionFrom an aeroplane vertically over a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be α and β. The height of the aeroplane above the road is
View SolutionFrom an aeroplane vertically over a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be α and β. The height of the aeroplane above the road is
View SolutionFrom an aeroplaneflying,vertically above a horizontal road,the angles of depression of two consecutive stones on the same side of aeroplane are observed to be 30∘ and 60∘ respectively.The height at which the aeroplane is flying in km is
View SolutionFrom an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive mile stones on opposite sides of the aeroplane are observed to be αandβ . Show that the height in miles of aeroplane above the road is give by tanαtanβtanα+tanβ
View SolutionFrom the top of a hill, the angles of depression of two consecutive kilometre stones due east are found to be 300and450 . Find the height of the hill.
View SolutionThe angles of elevation of an aeroplane from two places 10 km apart are found to be 60∘and30∘ respectively. Find the height of the aeroplane.
View SolutionFrom the top of the hill; the angle of depressions of two consecutive kilometre stones due east are found to be 30∘ and 45∘ . Find the height of the hill.
View SolutionFrom an aeroplane above a straight road the angles of depression of two positions at a distance 20 m apart on the road are observed to be 30∘and45∘. The height of the aeroplane above the ground is
View Solution