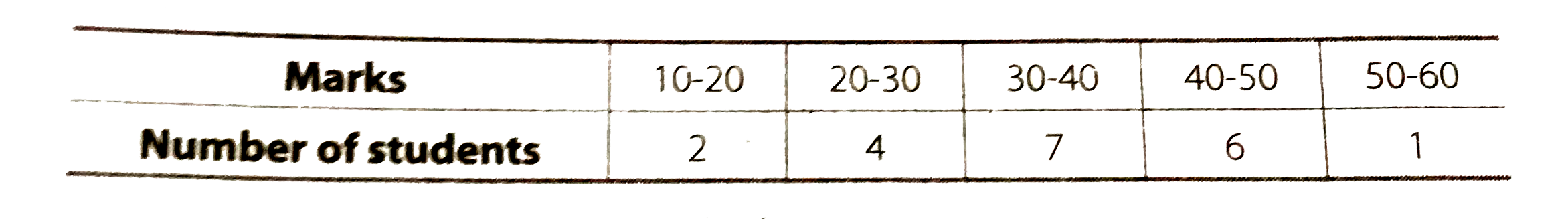The arithmetic mean of the scores of a group of students in a test was 52. The brightest 20% of them secured a mean score of 80 and the dullest 25% a mean score of 31. The mean score of remaining 55% is :
45
50
51.4 approx.
54.6approx.
The correct Answer is:C
To solve the problem step by step, we will use the information provided about the mean scores of different groups of students and set up an equation to find the mean score of the remaining 55% of students.
1. Identify the total number of students:
Let's assume the total number of students is 100 (this simplifies calculations since we are working with percentages).
2. Calculate the total score of all students:
The arithmetic mean of the scores of the entire group is 52. Therefore, the total score of all students can be calculated as:
Total Score=Mean×Number of Students=52×100=5200
3. Calculate the total score of the brightest 20% of students:
The brightest 20% of students is 20 students (20% of 100). Their mean score is 80, so their total score is:
Total Score of Brightest=80×20=1600
4. Calculate the total score of the dullest 25% of students:
The dullest 25% of students is 25 students (25% of 100). Their mean score is 31, so their total score is:
Total Score of Dullest=31×25=775
5. Calculate the total score of the remaining 55% of students:
The remaining 55% of students is 55 students (100 - 20 - 25 = 55). Let the mean score of these students be A. Therefore, their total score can be expressed as:
Total Score of Remaining=A×55
6. Set up the equation:
The total score of all students is the sum of the scores of the brightest, dullest, and remaining students:
1600+775+55A=5200
7. Combine and simplify the equation:
2375+55A=5200
8. Isolate A:
Subtract 2375 from both sides:
55A=5200−2375
55A=2825
9. Solve for A:
Divide both sides by 55:
A=282555≈51.3636
10. Final Answer:
Rounding to one decimal place, the mean score of the remaining 55% of students is approximately:
A≈51.4
Let's assume the total number of students is 100 (this simplifies calculations since we are working with percentages).
The arithmetic mean of the scores of the entire group is 52. Therefore, the total score of all students can be calculated as:
Total Score=Mean×Number of Students=52×100=5200
The brightest 20% of students is 20 students (20% of 100). Their mean score is 80, so their total score is:
Total Score of Brightest=80×20=1600
The dullest 25% of students is 25 students (25% of 100). Their mean score is 31, so their total score is:
Total Score of Dullest=31×25=775
The remaining 55% of students is 55 students (100 - 20 - 25 = 55). Let the mean score of these students be A. Therefore, their total score can be expressed as:
Total Score of Remaining=A×55
The total score of all students is the sum of the scores of the brightest, dullest, and remaining students:
1600+775+55A=5200
2375+55A=5200
Subtract 2375 from both sides:
55A=5200−2375
55A=2825
Divide both sides by 55:
A=282555≈51.3636
Rounding to one decimal place, the mean score of the remaining 55% of students is approximately:
A≈51.4
Similar Questions
Knowledge Check
The arithmetic mean of the scores of a group of students in a test was 52. The brightest 20% of them secured a mean score of 80 and the dullest 25% a mean score of 31.The mean score of remaining 55% is:
A54.6%/54.6% लगभगB0.45C0.5D51.4%/51.4% लगभगThe arithmetic mean of the scores of a group of students in a test was 52. The brightest 20% of them secured a mean score of 80 and the dullest 25% a mean score of 31. The mean score of remaining 55% is :
A45%B50%C51.4% (approx)D54.6% (approx)Question Stimulus :-
The average score of a group of students is 75. The brightest 28% of them secured an average score of 85 and the dullest 27% of them secured 38.The average score of remaining is ?A91B88C93D85
The following are the scores of two groups of class 9th students in a test of MATHEMATICS.
View SolutionThe mean score in a test of the 10 boys in a class was 15 while the overall mean of the 25 students in the class was 16.2. What was the mean score of the girls?
View SolutionThe arithmetic mean of the marks scored by student of a class is 58. 20 % of them secured a mean score of 60. The mean score of another 30% of the student was 40. The mean score of the remaining student is
View SolutionThe scores (out of 25) of 9 students in a Monday test are 14, 25, 17, 22, 20, 19, 10, 8 and 23. Find the sum of mean score and median score of the data.
View SolutionThe average score of 42 students in a test is 69. The ratio of the number of boysto that of girls is 10: 11. The average score of the boys is 20% more than that of the girls. The average score of the boys is :
View Solution