A uniform long tube is bent into a circle of radius R and it lies in vertical plane. Two liquids of same volume but densities ρ and δ fill half the tube. The angle θ is

tan−1(ρ−∂ρ+g)
tan−1ρg
tan−1∂ρ
tan−1(ρ+δρ+δ)
The correct Answer is:A
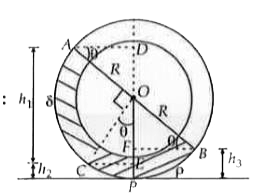
Vertical height of the liquid in portion AC
h1=DO+OE=Rsinθ+Rcosθ=R(sinθ+cosθ)
Vertical height of the liquid in portion CP
h2=R−Rcosθ=R(1−cosθ)
Vertical height of the liquid in portion PB
h3=R−Rsinθ=R(1−sinθ)
In equilibrium, the pressure due to liquid on the both sides must be equal at the lowest point P
∂gh1+ρgh2+ρgh3 [ as pressure =hρg]
∂gR(sinθ+cosθ)+ρgR(1−cosθ)=ρgR(1−sinθ)
∂(sinθ+cosθ)+ρ(1−cosθ)=ρ(1−sinθ)
(ρ+∂)sinθ=(ρ−∂)cosθ
tanθ=(ρ−δ)(ρ−δ)⇒θ=tan−1(ρ−gρ+g)
Topper's Solved these Questions
- BULK PROPERTIES OF MATTERBOOK - MTG-WBJEECHAPTER - BULK PROPERTIES OF MATTEREXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (SINGLE OPTION CORRECT TYPE)
22 Videos
- BULK PROPERTIES OF MATTERBOOK - MTG-WBJEECHAPTER - BULK PROPERTIES OF MATTEREXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (ONE OR MORE THAN ONE OPTION CORRECT TYPE)
1 Videos
- BULK PROPERTIES OF MATTERBOOK - MTG-WBJEECHAPTER - BULK PROPERTIES OF MATTEREXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (ONE OR MORE THAN ONE OPTION CORRECT TYPE)
1 Videos
- ATOMS MOLECULES AND CHEMICAL ARITHEMETIC BOOK - MTG-WBJEECHAPTER - ATOMS MOLECULES AND CHEMICAL ARITHEMETIC EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS CATEGORY 1: SINGLE OPTION CORRECT TYPE (1 MARK)
3 Videos
- CURRENT ELECTRICITY BOOK - MTG-WBJEECHAPTER - CURRENT ELECTRICITY EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS
21 Videos
Similar Questions
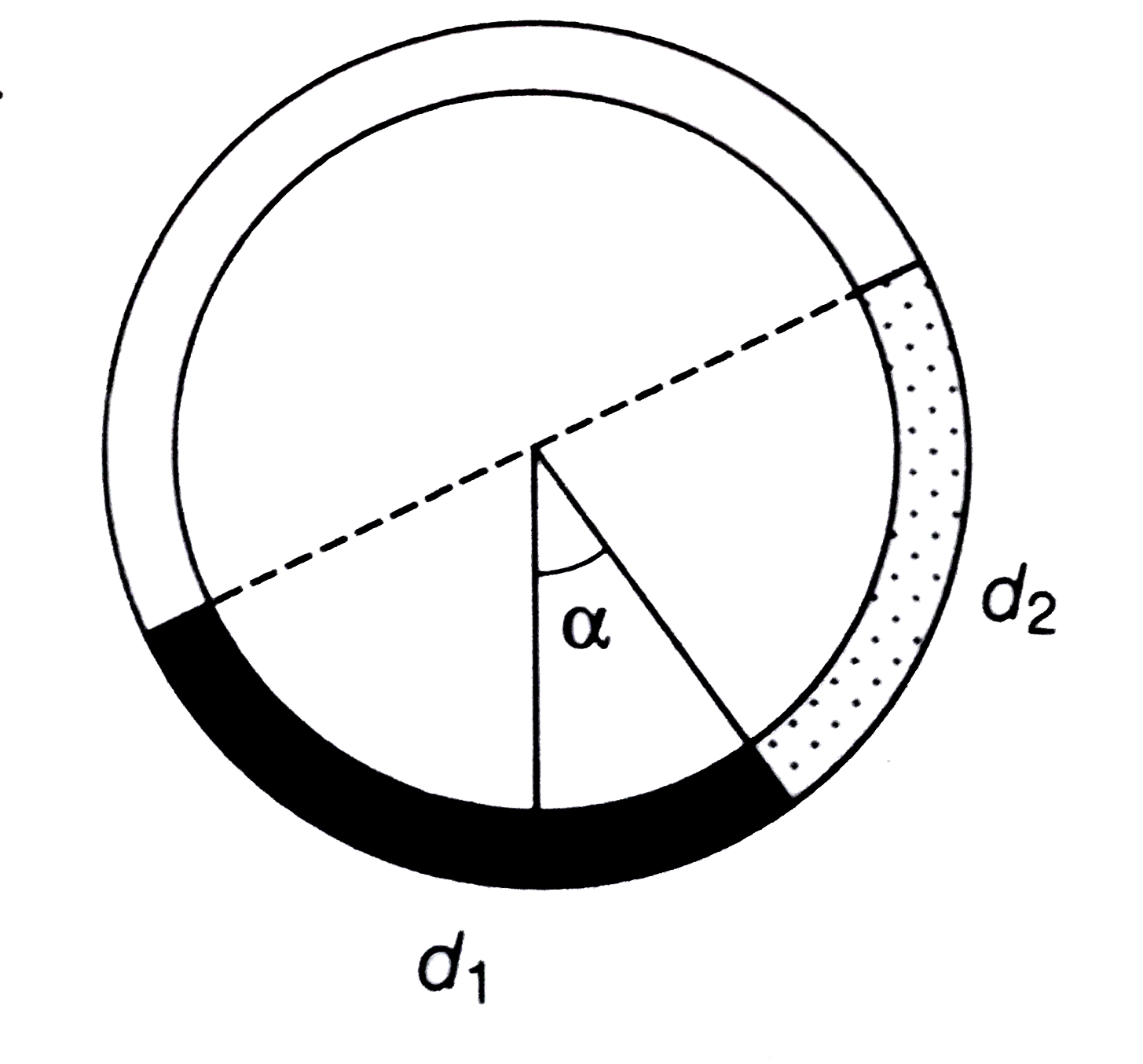
There is a circular tube in a vertical plane. Two liquids which do not mix and of densiities d1andd2 are filled I the tube. Each liquid subtends 90∘ angle at centre. Radius joining their interface makes an angle α with vertical. Ratio d1/d2 is
View SolutionWhen one end of a tube of radius r is immersed vertically in a liquid of density ρ, surface tension S, the rise of liquid in the tube is h and angle of contact is θ . If the tube is broken and its length is made h'(<h), then find the value of height of rise of liquid in the tube and angle of contact.
View Solution
Knowledge Check
A small uniform tube is bent into a circle of radius r whose plane is vertical. Equal volumes of two fluids whose densities areρ and σ(ρ>σ) fill half the circle. Find the angle that the radius passing through the interface makes with the vertical.
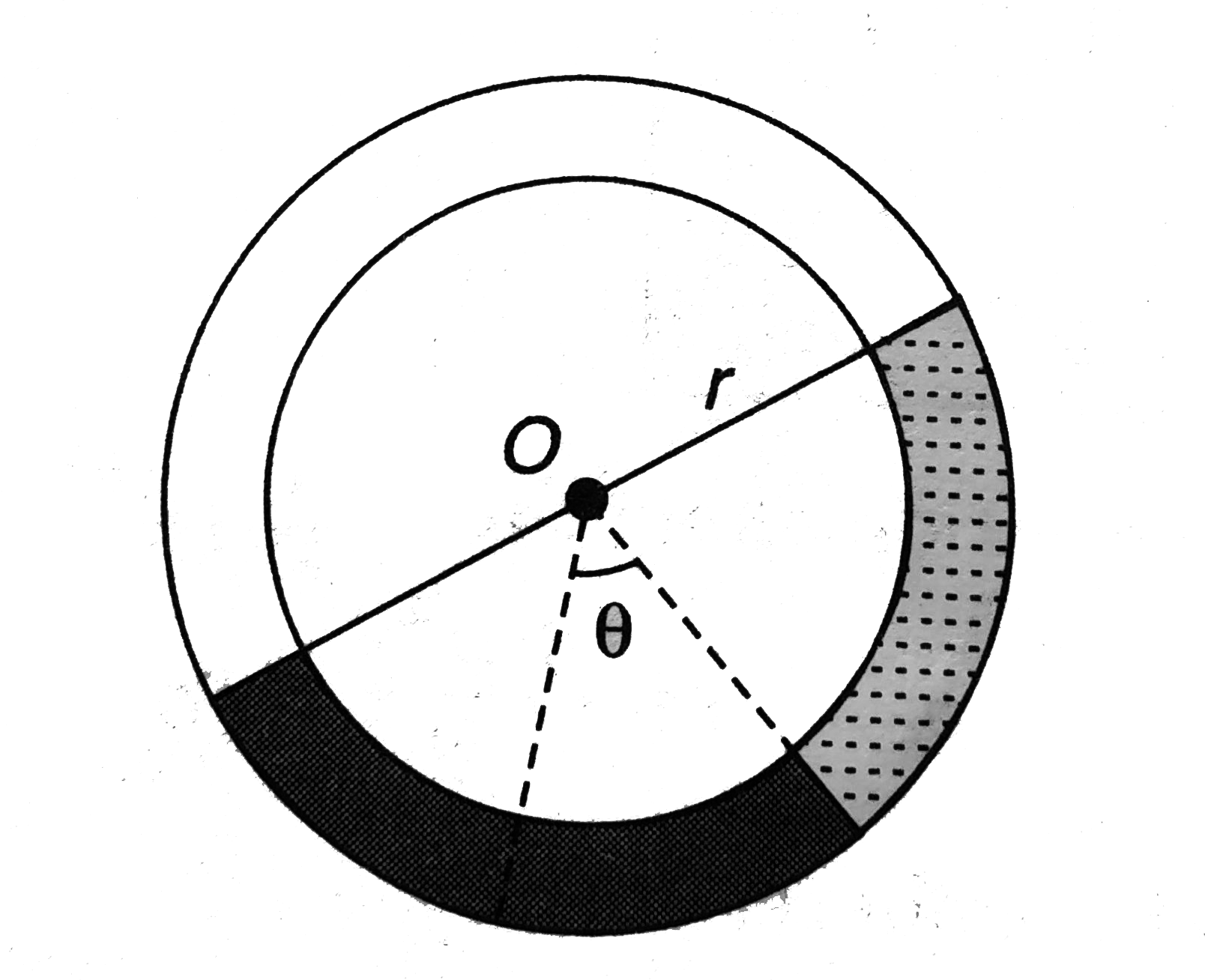 Atan−1(ρ+σρ−σ)Btan−1(ρ−σρ−σ)Ctan−1(ρ+σρ+σ)Dtan−1(ρ−σρ+σ)
Atan−1(ρ+σρ−σ)Btan−1(ρ−σρ−σ)Ctan−1(ρ+σρ+σ)Dtan−1(ρ−σρ+σ)A thin uniform tube is bent into a circle of radius r in the vertical plane. Equal volumes of two immiscible liquids, whose densities are ρ1 and ρ2(ρ1>ρ2) fill half the circle. The angle θ between the radius vector passing though the common interface and the vertical is :
Aθ=tan−1'π2(ρ2ρ1)Bθ=tan−1'π(ρ1ρ2)Cθ=tan−1'π2(ρ1+ρ2ρ1−ρ2)Dθ=tan−1'[π2(ρ1+ρ2ρ1−ρ2)]If two liquids of same volume but different densities ρ1 and ρ2 are mixed, then the density of the mixture is:
Aρ=ρ1+ρ22Bρ=ρ1+ρ22ρ1ρ2Cρ=2ρ1ρ2ρ1+ρ2Dρ=ρ1ρ2ρ1+ρ2
Two non-viscous, incomoressible and immiscible liquids of densities ρ and 1.5ρ are poured into the two limbs of a circules tube of radius R and small cross-section kept fixed in a vertical plane as shown in fig. Each liquid occupies one-fourth the cirumference of the tube.

(a) Find the angle θ the radius to the interface makes with the vertical in equilibrium position.
(b) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations alre simple harmonic. Find the time period of these oscillations.
View SolutionIf two liquids of same volume but different densities ρ1andρ2 are mixed, then density of mixture is given by
View SolutionIf two liquids of same volume but different densities ρ1andρ2 are mixed, then density of mixture is given by
View SolutionA thin uniform circular tube is kept in a vertical plane. Equal volume of two immiscible liquids whose densites are ρ1 and ρ2 fill half of the tube as shown. In equilibrium the radius passing through the interface makes an angle of 30∘ with vertical. The ratio of densities (ρ1/ρ2) is equal to

View SolutionThere is a circular tube in a vertical plane. Two liquids which do not mix and of densities d1andd2 are filled in the tube. Each liquid substends 90∘ angle at centre. Radius joining their interface make an angle α with vertical. Ratio d1d2 is :
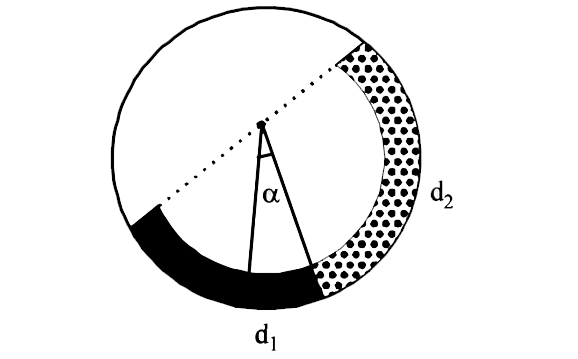
View Solution
