Prove that the diagonals of a rectangle ABCD with vertices A(2, -1), B(5, -1), C(5, 6) and D(2, 6) are equal and bisect each other.

Video Solution

Text Solution

Verified by Experts

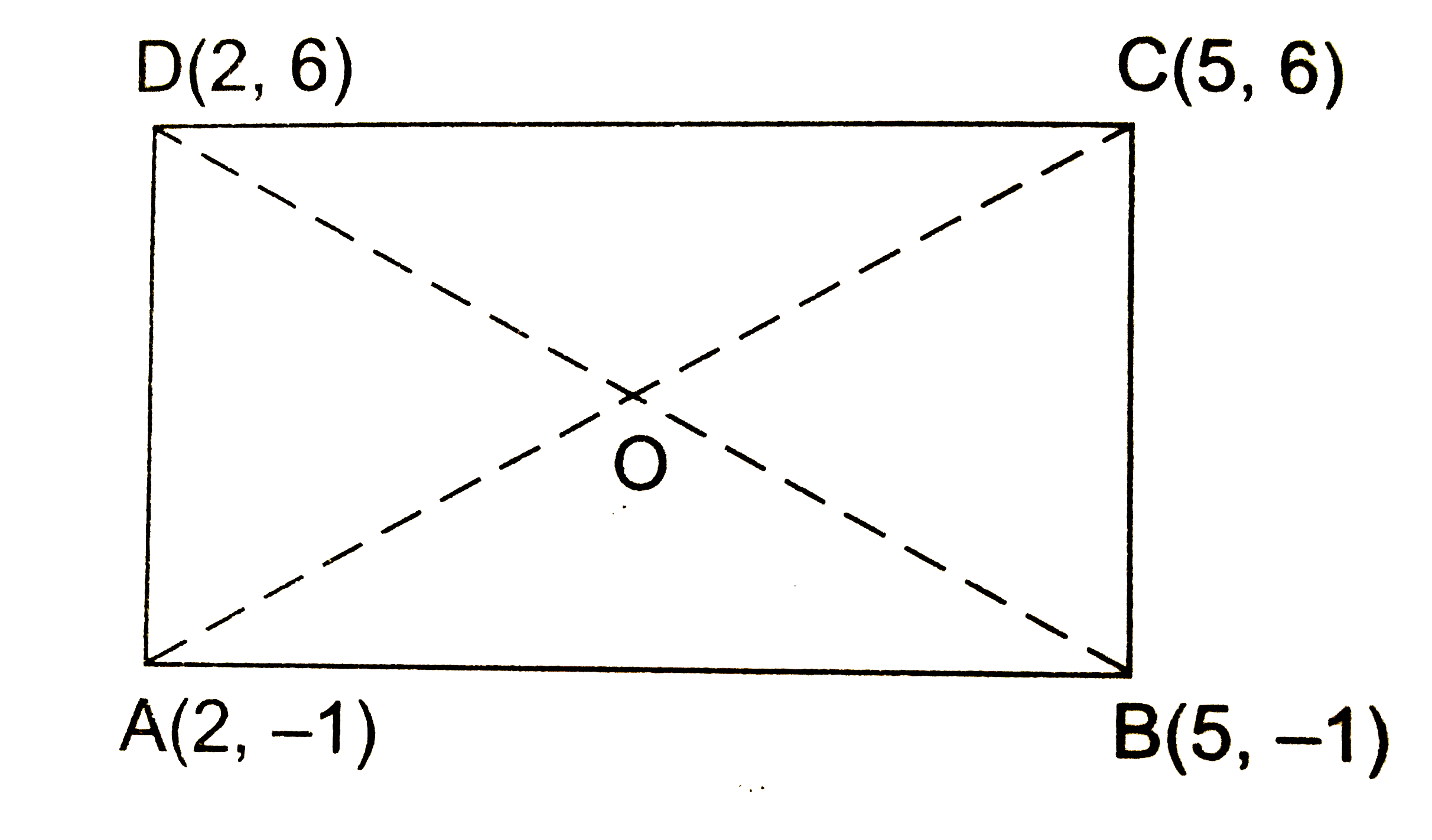
Diagonal $A C = \sqrt{{(5 - 2)}^{2} + {(6 + 1)}^{2}}$
$= \sqrt{3^{2} + 7^{2}} = \sqrt{9 + 49} = \sqrt{58}$
Diagonal $B D = \sqrt{{(5 - 2)}^{2} + {(- 1 - 6)}^{2}}$
$= \sqrt{3^{2} + {(- 7)}^{2}} = \sqrt{9 + 49} = \sqrt{58}$
$∴$ Diag. AC = Diag. BD.
Midpoint of $A C = (\frac{5 + 2}{2}, \frac{6 - 1}{2}) = (\frac{7}{2}, \frac{5}{2})$
Midpoint of $B D = (\frac{5 + 2}{2}, \frac{- 1 + 6}{2}) = (\frac{7}{2}, \frac{5}{2})$

Updated on:21/07/2023

Find the area of a rectangle whose vertices are A(-2, 6), B (5,3), C (-1,-11) and D(-8,-8)
A $4 \sqrt{29}$ sq. units
B116 sq. units
C $29 \sqrt{5}$ sq. units
D $58 \sqrt{2}$ sq. units
The area of the quadrilateral ABCD where A(0,4,1), B(2,3,-1), C(4,5,0) and D(2,6,2), is equal to
A9 sq.units
B18 sq. units
C27 sq. units
D81 sq.units
The area of the quadrilateral ABCD where $A (0, 4, 1), B (2, 3, - 1), c (4, 5, 0) and D (2, 6, 2)$ is to :
A9 sq units
B18 sq units
C27 sq units
D81 sq units