The base QR of an equilateral triangle PQR lies on x-axis. The coordinates of the point Q are (−4,0) and origin is the midpoint of the base. Find the coordinates of the points P and R.
P(0,5√4)orP(0,−5√4)andR(3,2)
P(0,4√3)orP(0,−4√3)andR(4,0)
P(0,3√2)orP(0,−3√2)andR(3,1)
P(0,2√5)orP(0,−2√5)andR(3,5)
The correct Answer is:B
To find the coordinates of points P and R in the equilateral triangle PQR, we can follow these steps:
Step 1: Identify the coordinates of Q and the midpoint of QR
- The coordinates of point Q are given as Q(-4, 0).
- The origin (0, 0) is the midpoint of the base QR.
Step 2: Use the midpoint formula to find the coordinates of R
The midpoint formula states that the midpoint M of a line segment with endpoints (x1, y1) and (x2, y2) is given by:
M=(x1+x22,y1+y22)
Here, the midpoint is (0, 0), and we know Q(-4, 0). Let the coordinates of R be (x, 0).
Using the midpoint formula:
0=−4+x2
This implies:
−4+x=0
x=4
Thus, the coordinates of point R are R(4, 0).
Step 3: Determine the length of QR
The distance QR can be calculated as:
QR=|x2−x1|=|4−(−4)|=|4+4|=8
Step 4: Find the height of the equilateral triangle
In an equilateral triangle, the height can be calculated using the formula:
h=√32×side length
Here, the side length is QR, which is 8.
Thus, the height (h) is:
h=√32×8=4√3
Step 5: Determine the coordinates of point P
Since point P is directly above the midpoint of QR (which is the origin (0, 0)), the coordinates of P will be:
P(0,h)=(0,4√3)
Final Coordinates
- The coordinates of point P are P(0,4√3)
- The coordinates of point R are R(4,0)
Summary of Coordinates
- Q: (-4, 0)
- R: (4, 0)
- P: (0, 4√3)
---
- The coordinates of point Q are given as Q(-4, 0).
- The origin (0, 0) is the midpoint of the base QR.
The midpoint formula states that the midpoint M of a line segment with endpoints (x1, y1) and (x2, y2) is given by:
M=(x1+x22,y1+y22)
0=−4+x2
This implies:
−4+x=0
x=4
The distance QR can be calculated as:
QR=|x2−x1|=|4−(−4)|=|4+4|=8
In an equilateral triangle, the height can be calculated using the formula:
h=√32×side length
Here, the side length is QR, which is 8.
h=√32×8=4√3
Since point P is directly above the midpoint of QR (which is the origin (0, 0)), the coordinates of P will be:
P(0,h)=(0,4√3)
- The coordinates of point P are P(0,4√3)
- The coordinates of point R are R(4,0)
- Q: (-4, 0)
- R: (4, 0)
- P: (0, 4√3)
Topper's Solved these Questions
- COORDINATE GEOMETRYBook:RS AGGARWALChapter:COORDINATE GEOMETRYExercise:Exercise 6C
Explore 24 Videos
- COORDINATE GEOMETRYBook:RS AGGARWALChapter:COORDINATE GEOMETRYExercise:Exercise 6D
Explore 17 Videos
- COORDINATE GEOMETRYBook:RS AGGARWALChapter:COORDINATE GEOMETRYExercise:Exercise 6A
Explore 34 Videos
- CONSTRUCTIONSBook:RS AGGARWALChapter:CONSTRUCTIONSExercise:Test Yourself
Explore 10 Videos
- HEIGHTS AND DISTANCESBook:RS AGGARWALChapter:HEIGHTS AND DISTANCESExercise:Multiple Choice Questions (Mcq)
Explore 25 Videos
Similar Questions
The base QR of an equilateral triangle PQR lies on X-axis. The co-ordinates of the point Q are (-4,0) and origin is the mid-point of the base. Find the co-ordinates of the points P and R.
View SolutionThe base BC of an equilateral triangle ABC, lies on y-axis. The coordinates of point C are (0, -3). The origin is the midpoint of the base.
Find the coordinates of the points A and B.
View Solution
Knowledge Check
A point E with x-coordinate 4 lies on the line segment joining the point P(2,−3,4) and Q(8,0,10). Find the coordinates of the point R
A(4,−2,−6)B(4, 2, 6)C(4,−2,6)DNone of the these
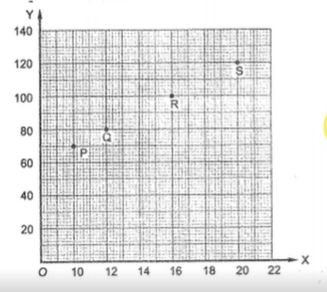
Find the coordinates of points P, Q, R and S in Figure.
View SolutionThe base of an equilateral triangle with side 20cm lies along x-axis such that the mid-point of the base is at the origin. Find the vertices of the triangle
View SolutionIf the point P lies on Z - axis , then coordinates of p are of the form ……….
View SolutionThe base of an equilateral triangle with side 2a lies along the y–axis such that the mid–point of the base is at the origin. Find vertices of the triangle.
View SolutionThe base of an equilateral triangle with side 2a lies along the y-axis such that the mid point of the base is at the origin. Find the vertices of the triangle.
View SolutionA point R with x-coordinates 4 lies on the line segment joining the points P(2,−3,4)and Q(8,0,10). Find the coordinates of the point R
View SolutionThe coordinates of the point P are (−3, 2) . Find the coordinates of the point Q which lies on the line joining P and origin such that OP=OQ .
View Solution