Find the area of the triangle formed by joining the midpoints of the sides of the triangle whose vertices are A(2, 2), B(4, 4) and C(2, 6).
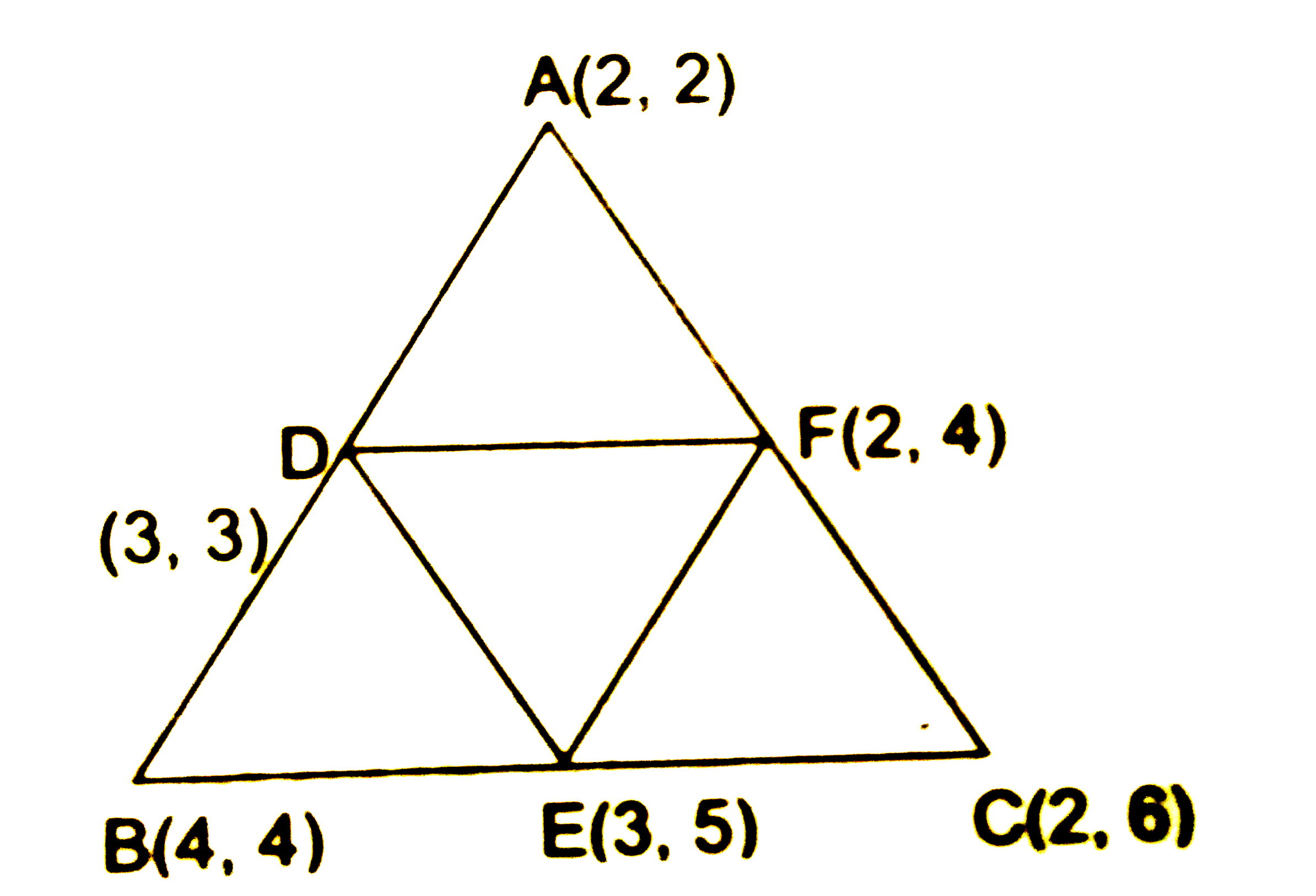
Let A(2, 2) B(4, 4) and C(2, 6) be the vertices of the given ΔABC. Let D, E and F be the midpoints of AB, BC and CA respectively.
Then, the coordinates of D,E and F are
D(2+42,2+42),E(4+22,4+62) and F(2+22,2+62),i.e.,D(3,3),E(3,5) and F(2,4).
For ΔDEF, we have
(x1=3,y1=3),(x2=3,y2=5) and (x3=2,y3=4).
∴ar(ΔDEF)=12|x1(y2−y1)+x2(y3−y1)+x3(y1−y2)|
=12|3⋅(5−4)+3⋅(4−3)+2⋅(3−5)|
=12|(3×1)+(3×1)+2×(−2)|
=12|3+3−4|=(12×2)=1 sq units.
Hence, the are of ΔDEF is 1 sq unit.
Topper's Solved these Questions
- COORDINATE GEOMETRYBook:RS AGGARWALChapter:COORDINATE GEOMETRYExercise:Exercise 6A
Explore 34 Videos
- COORDINATE GEOMETRYBook:RS AGGARWALChapter:COORDINATE GEOMETRYExercise:Exercise 6B
Explore 38 Videos
- CONSTRUCTIONSBook:RS AGGARWALChapter:CONSTRUCTIONSExercise:Test Yourself
Explore 10 Videos
- HEIGHTS AND DISTANCESBook:RS AGGARWALChapter:HEIGHTS AND DISTANCESExercise:Multiple Choice Questions (Mcq)
Explore 25 Videos
Similar Questions
Find the area of the triangle formed by joining the midpoints of the sides of the triangle whose vertices are A(2, 1), B(4, 3) and C(2, 5).
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle, whose vertices are (2, - 4), (6, 2) and (- 4, 6). Find the ratio of this area to the area of the given triangle.
View Solution
Knowledge Check
The area of the triangle whose vertices are A(1,2−1) B (3,1,4) and C (0,2,3)
A√1762sp unitB8 sq unitC√1862 sq unitDNone of theseFind the area of the triangle, whose vertices are (2,1), (4,5) and (6,3).
A3B6C9D12
Find the area of the triangle formed by joining the mid–points of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
View SolutionFind the area of the triangle formed by joining the mid -points of the sides of the triangle ABC ,whose vertices are A(0,-1),B(2,1)andC(0,3).
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0,−1),(2,1)and(0,3). Find the ratio of this area to the area of the given triangle.
View SolutionFind the area of the triangle formed by the mid points of sides of the triangle whose vertices are (2,1),1−2,3),(4,−3)
View SolutionFind the equation of the sides of the triangle whose vertices are (2,1),(−2,3)and(4,5)
View SolutionFind the area of the triangle whose vertices are A(1, 2, 3), B(2, –1, 1)and C(1, 2, –4).
View Solution

