If $A (4, - 6), B (3, - 2) a n d C (5, 2)$ are the vertices of $A B C,$ then verify the fact that a median of a triangle ABC divides it into two triangles of equal areas.

Video Solution

Text Solution

Verified by Experts

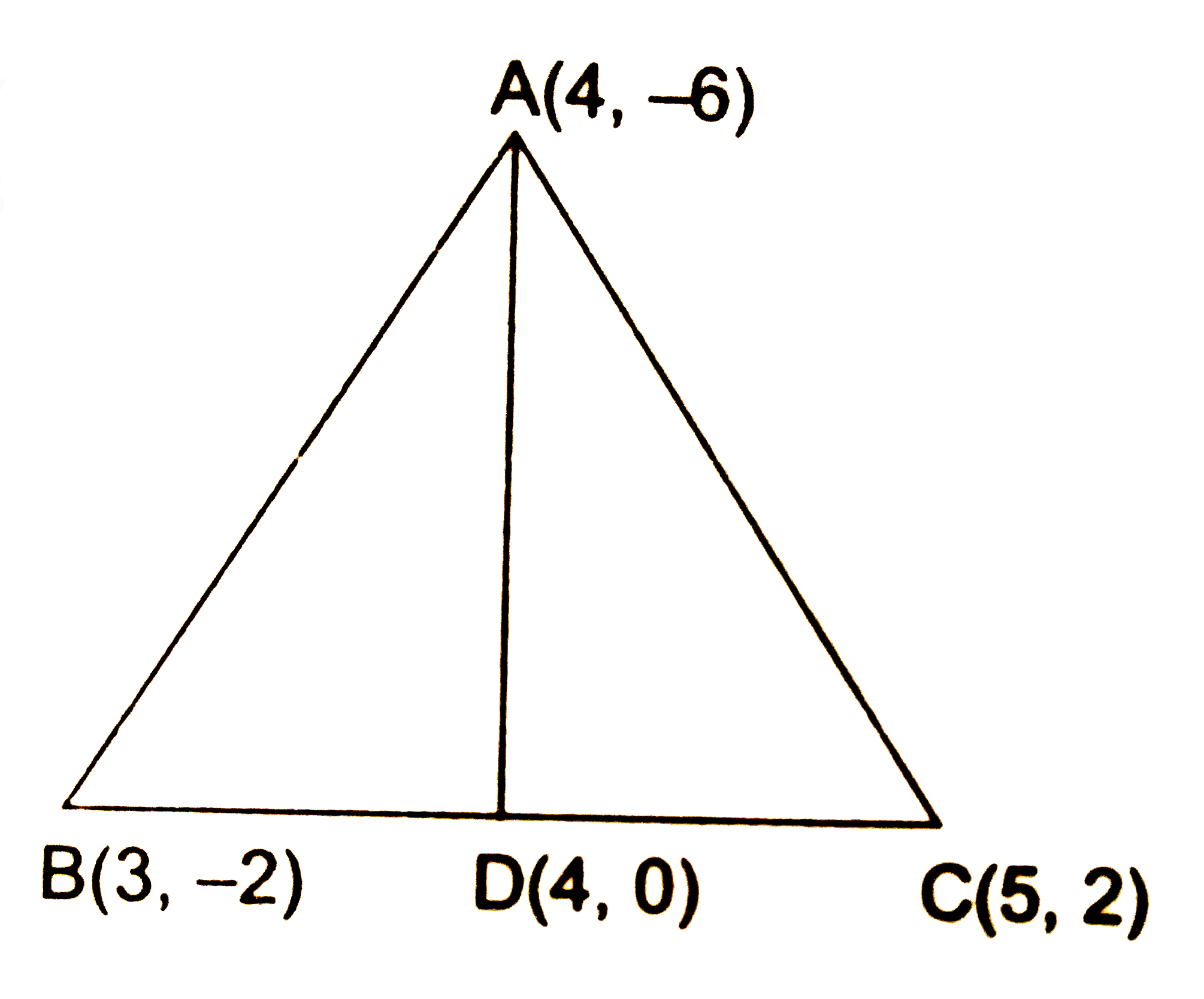
It is being given that A(4, -6), B(3, -2) and C(5, 2) are the vertices of a $Δ A B C$ and AD is its median. Clearly, D is the midpoint of BC.
$∴$ the coordinates of D are $(\frac{3 + 5}{2}, \frac{- 2 + 2}{2}) = (4, 0) .$
For $Δ A B D$ , we have
$A (x_{1} = 4, y_{1} = - 6), B (x_{2} = 3, y_{2} = - 2) and D (x_{3} = 4, y_{3} = 0) .$
$a r (Δ A B D) = \frac{1}{2} | x_{1} (y_{2} - y_{3}) + x_{2} (y_{3} - y_{1}) + x_{3} (y_{1} - y_{2}) |$
$= \frac{1}{2} | 4 \cdot (- 2 - 0) + 3 \cdot (0 + 6) + 4 \cdot (- 6 + 2) |$
$= \frac{1}{2} | 4 \times (- 2) + 3 \times 6 + 4 \times (- 4) |$
$= \frac{1}{2} | - 8 + 18 - 16 | = \frac{1}{2} | - 6 |$
$= (\frac{1}{2} \times 6) = 3$ sq units.
For $Δ A D C$ , we have
$(x_{1} = 4, y_{1} = - 6), (x_{2} = 4, y_{2} = 0) and (x_{3} = 5, y_{3} = 2) .$
$∴ a r (Δ A D C) = \frac{1}{2} | x_{1} (y_{2} - y_{3}) + x_{2} (y_{3} - y_{1}) + x_{3} (y_{1} - y_{2}) |$
$= \frac{1}{2} | 4 \cdot (0 - 2) + 4 \cdot (2 + 6) + 5 \cdot (- 6 - 0) |$
$= \frac{1}{2} | 4 \times (- 2) + 4 \times 8 + 5 \times (- 6) |$
$= \frac{1}{2} | - 8 + 32 - 30 | = \frac{1}{2} | - 6 |$
$= (\frac{1}{2} \times 6) = 3$ sq units.
$∴ a r (Δ A B D) = a r (Δ A D C)$
Hene, the median AD divides $Δ A B C$ into two triangles of equal areas.

Updated on:21/07/2023

|

Class 10 MATHS COORDINATE GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

If A (1,-2), B (-2,3) and C(2,-5) are the vertices of $Δ$ ABC, then the equation of the median BE is
A7x+13y+47=0
B13x+7y+5=0
C7x-13y+5=0
Dnone of these

RS AGGARWAL-COORDINATE GEOMETRY-Multiple Choice Questions (Mcq)

Home
Ask Doubt
Profile