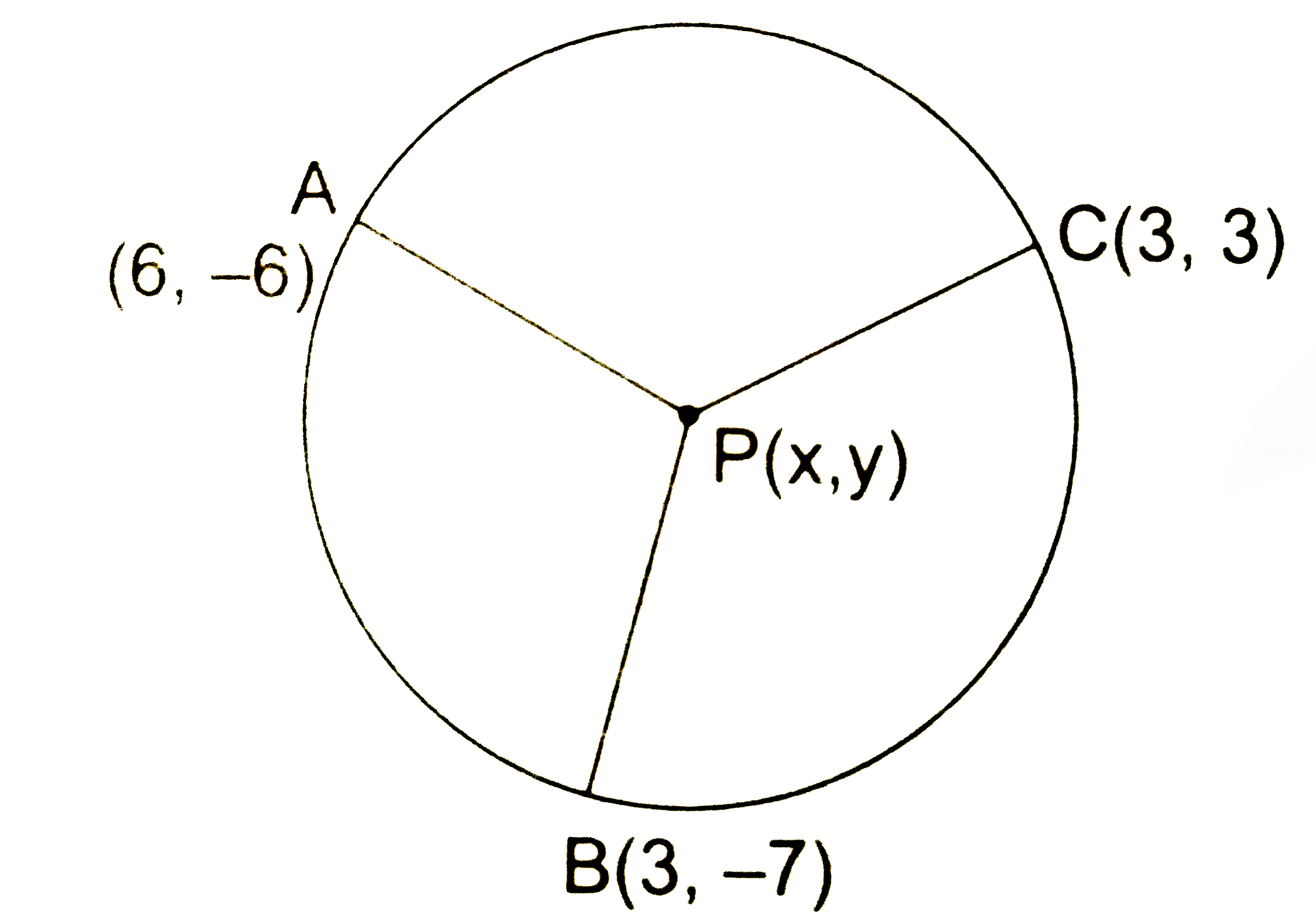
Find the centre of the circle passing through $(6, - 6), (3, - 7)$ and $(3, 3)$ .

A

(3, 1)

B

(-3, -1)

C

(-3, 1)

D

(3, -2)

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Let P(x, y) be the centre of a circle passing through the points A(6, -6), B(3, -7) and C(3, 3). Then,
$P A^{2} = P B^{2} and P B^{2} = P C^{2}$

$\Rightarrow {\begin{matrix} {(x - 6)}^{2} + {(y + 6)}^{2} = {(x - 3)}^{2} + {(y + 7)}^{2} {(x - 3)}^{2} + {(y + 7)}^{2} = {(x - 3)}^{2} + {(y - 3)}^{2} \end{matrix}$
$\Rightarrow ⎧ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎩ \begin{matrix} x^{2} + y^{2} - 12 x + 12 y + 72 = x^{2} + y^{2} - 6 x + 14 y + 58 x^{2} + y^{2} - 6 x + 14 y + 58 = x^{2} + y^{2} - 6 x - 6 y + 18 \end{matrix}$
$\Rightarrow$ 6x+2y = 14 and 20y = -2
$\Rightarrow$ 3x+y =7 and y = -2
$\Rightarrow$ x = 3 and y = -2.
Hence, the centre of the circle is P (3, -2).

Updated on:21/07/2023

|

Class 10 MATHS COORDINATE GEOMETRY

Topper's Solved these Questions

Similar Questions

RS AGGARWAL-COORDINATE GEOMETRY-Multiple Choice Questions (Mcq)

Home
Ask Doubt
Profile