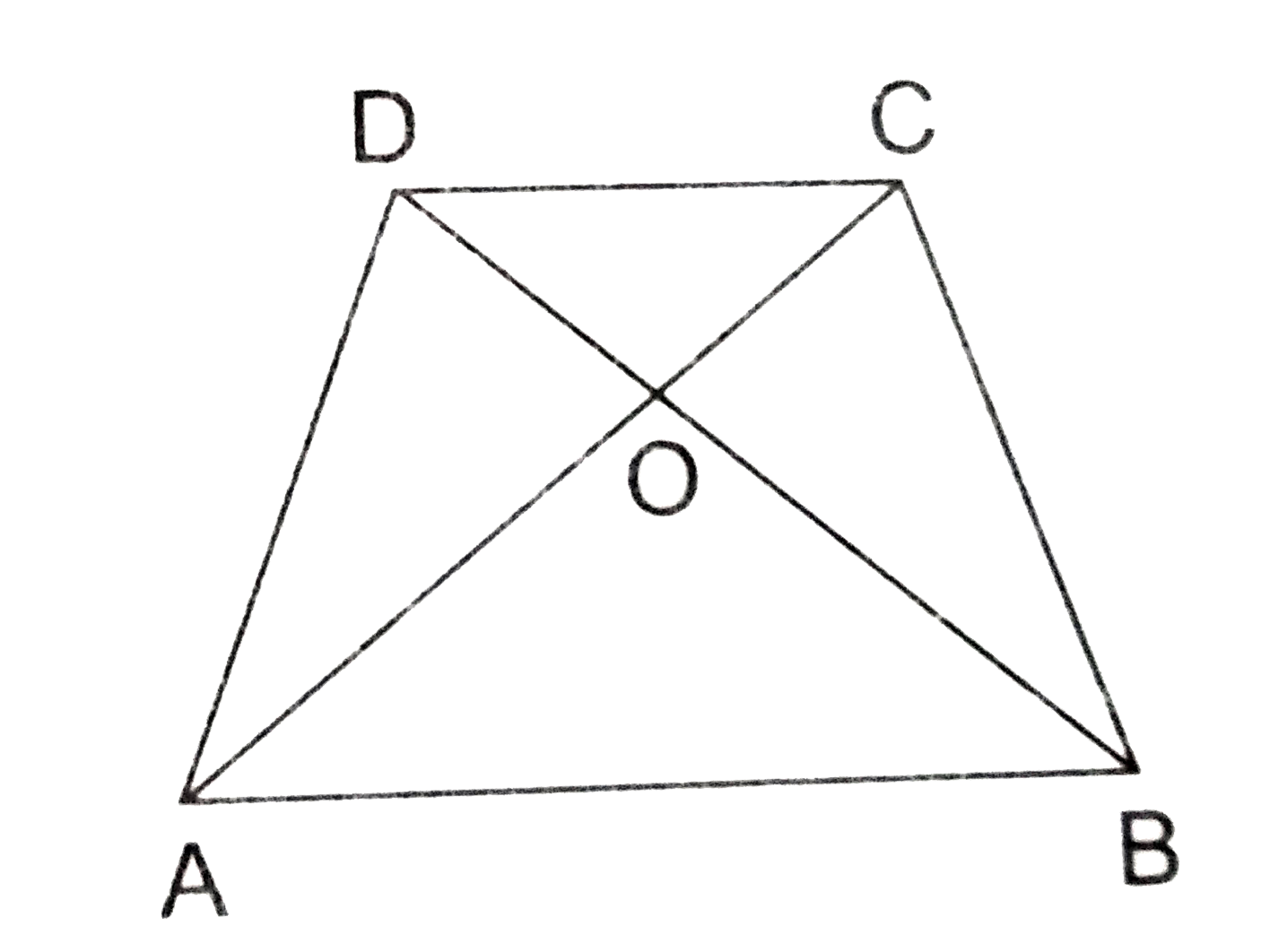
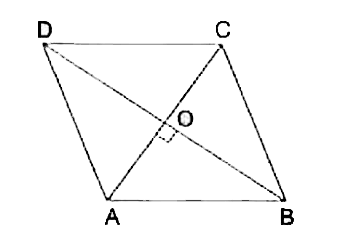
In the given figure, ABCD is trapezium whow diagonals AC and BD intersect at O such that OA=(3x−1)cm,(OB=(2x+1)cm,OC=(5x−3)cmandOD=(6x−5)cm. Then, x=?
The correct Answer is:A
We know that the diagonals of trapezium divide each other proportionally.
∴OAOC=OBOD⇒3x−15x−3=2x−16x−5
⇒(3x−1)(6x−5)=(5x−3)(2x+1)
⇒18x2−21x+5=10x2−x−3⇒8x2−20x+8=0
⇒2x2−5x+2=0⇒2x2−4x+2=0⇒2x(x−2)−(x−2)=0
⇒(x−2)(2x−1)=0⇒x=2orx=12
But, x=12 gives (6x−5)<0 and the distance cannot be negative .
∴x=2
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:MULTPILE-CHOICE QUESTIONS (MCQ) ( MATCHING OF COLUMNS)
Explore 1 Video
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Test Yourself
Explore 20 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Exercise 7E
Explore 30 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
In the adjoining figure, ABCD is a trapezium in which CD∣∣AB and its diagonals intersect at O. if AO=(5x−7)cm,OC=(2x+1)cm,BO=(7x−5)cmandOD=(7x+1)cm, find the value of x.
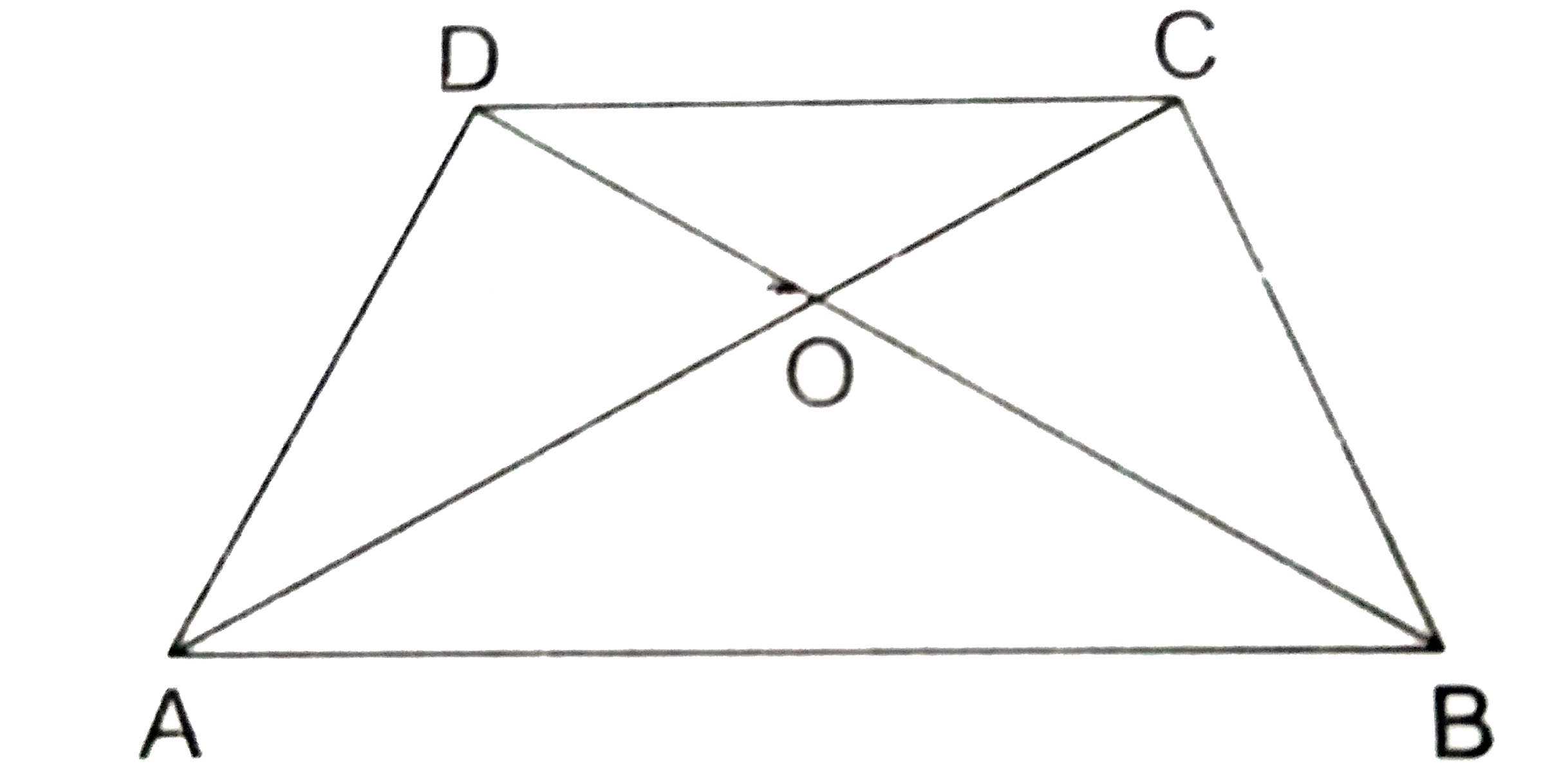
View SolutionIn the given fig., AB || DC and diagonals AC and BD intersects at O. If OA =3x-1 and OB =2x + 1, OC = 5x-3 and OD =6x-5, find the value of x.
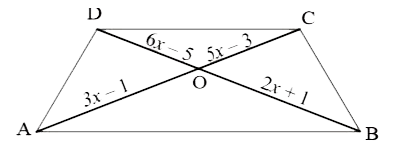
View Solution
Knowledge Check
In the given figure, ABCD is a ||gm in which diagonals AC and BD intersect at O. If ar(||gm ABCD) is 52cm2 then the ar(△AOB)=?
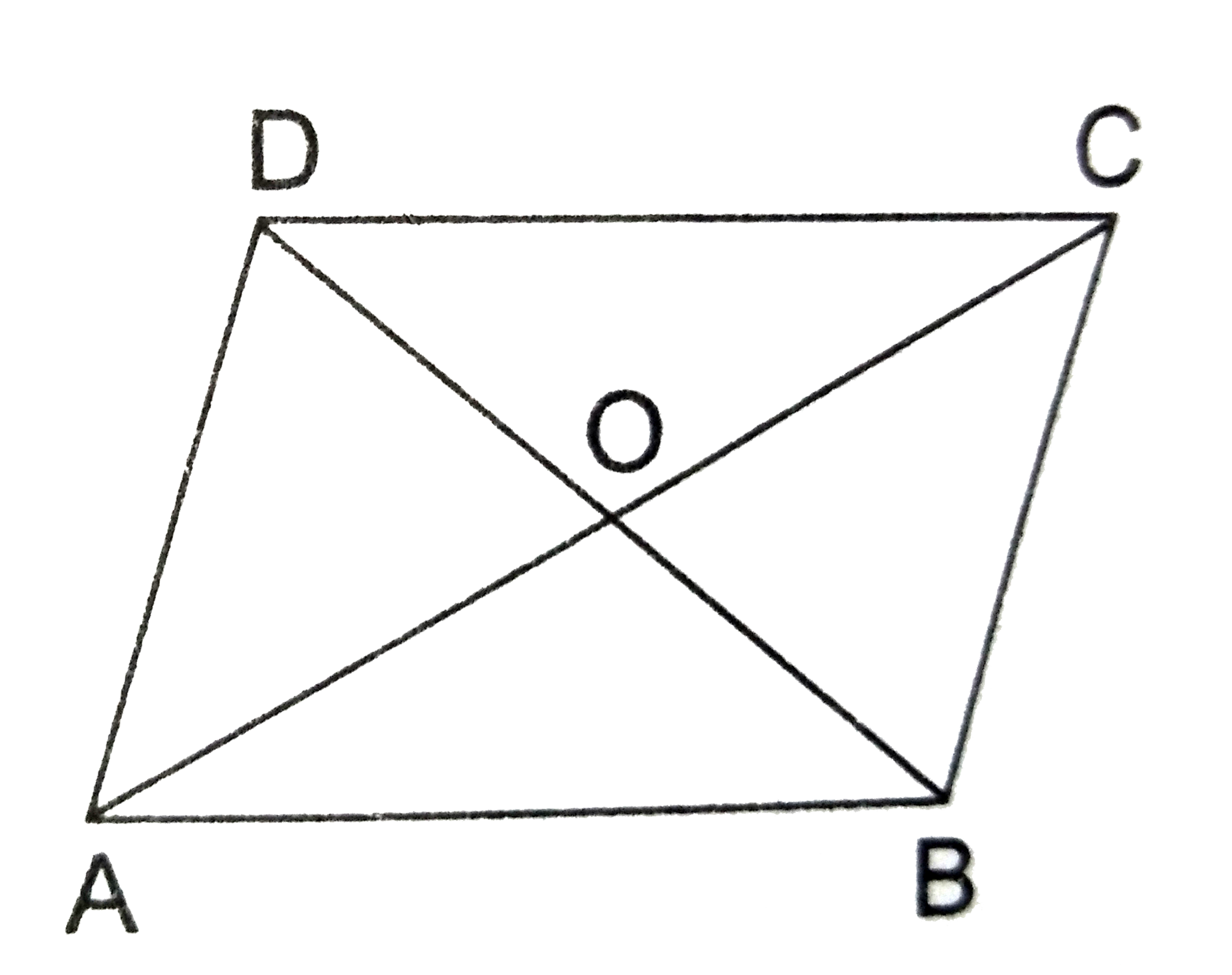 A26cm2B18.5cm2C39cm2D13cm2
A26cm2B18.5cm2C39cm2D13cm2ABCD is a trapezium in which AB parallel to DC and its diagonals intersect at P. If AP = (3x - 1) cm, PC = (5x - 3) cm, BP = (2x + 1) cm and PD = (6x - 5) cm, then the length of DB is:
ABCD एक समलम्ब है जिसमें AB, DC के समानांतर है तथा इसके विकर्ण P पर एक दूसरे को काठते हैं | यदि AP = (3x - 1) सेमी, PC = (5x - 3) सेमी, BP = (2x + 1) सेमी तथा PD = (6x - 5) सेमी है, तो DB की लंबाई क्या होगी ?A14 cmB12 cmC10 cmD16 cm
In the adjoining figure, ABCD is a trapezium in which CD∣∣AB and its diagonals intersect at O. If AO=(5x−7)cm,OC=(2x+1)cm,DO=(7x−5)cm and OB=(7x+1)cm, find the value of x.
View SolutionABCD is a trapezium in which AB parallel to DC and its diagonals intersect at P. If AP = (3x - 1) cm, PC = (5x - 3) cm, BP = (2x + 1) cm and PD = (6x - 5) cm, then the length of DB is:
ABCD एक समलम्ब है जिसमें AB, DC के समानांतर है तथा इसके विकर्ण P पर एक दूसरे को काठते हैं | यदि AP = (3x - 1) सेमी, PC = (5x - 3) सेमी, BP = (2x + 1) सेमी तथा PD = (6x - 5) सेमी है, तो DB की लंबाई क्या होगी ?
View SolutionIn the adjacent figure , ABCD is a rhombus whose diagonals AC and BD intersect at a point O. If side AB=10 cm and diagonal BD=16 cm , find the length of diagonal AC.
View SolutionIn the given figure, DE∣∣BC such that AD=xcm,DB=(3x+4)cm,AE=(x+3)cmandEC=(3x+19)cm. Find the value of x.
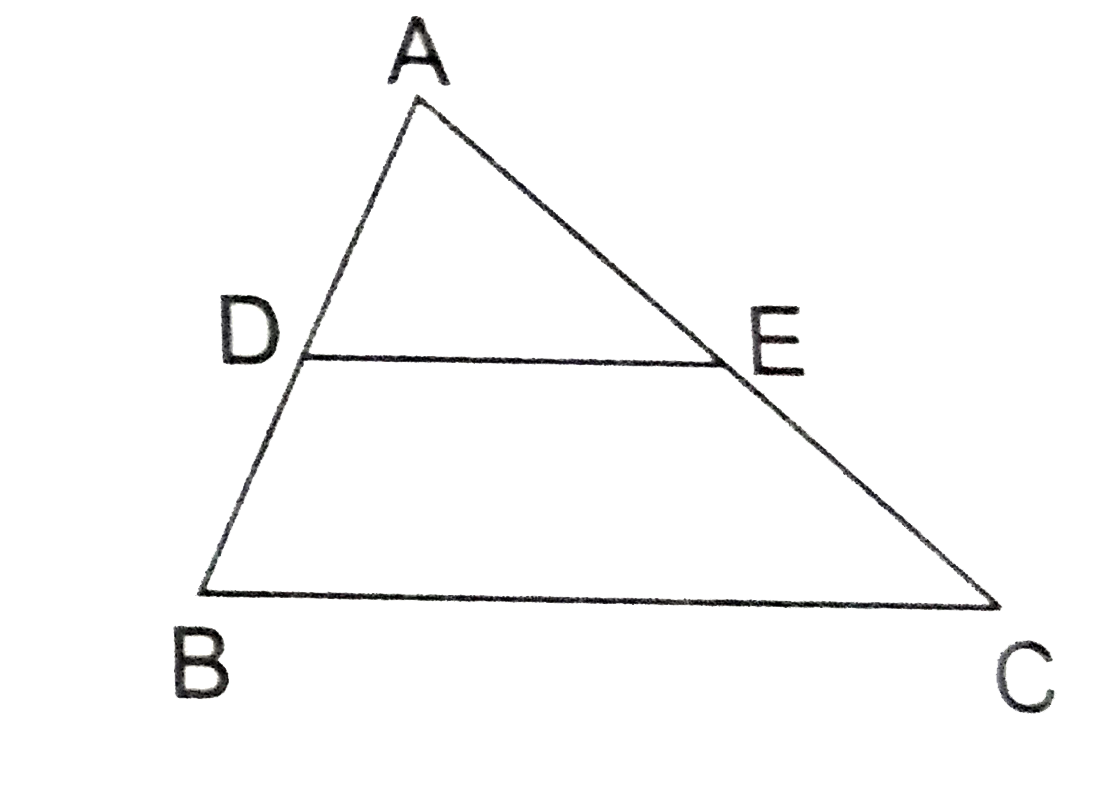
View SolutionIn ΔABC,DE∣∣BC so that AD=(7x−4)cm,AE=(5x−2)cm,DB=(3x+4)cmandEC=3x. Then, we have
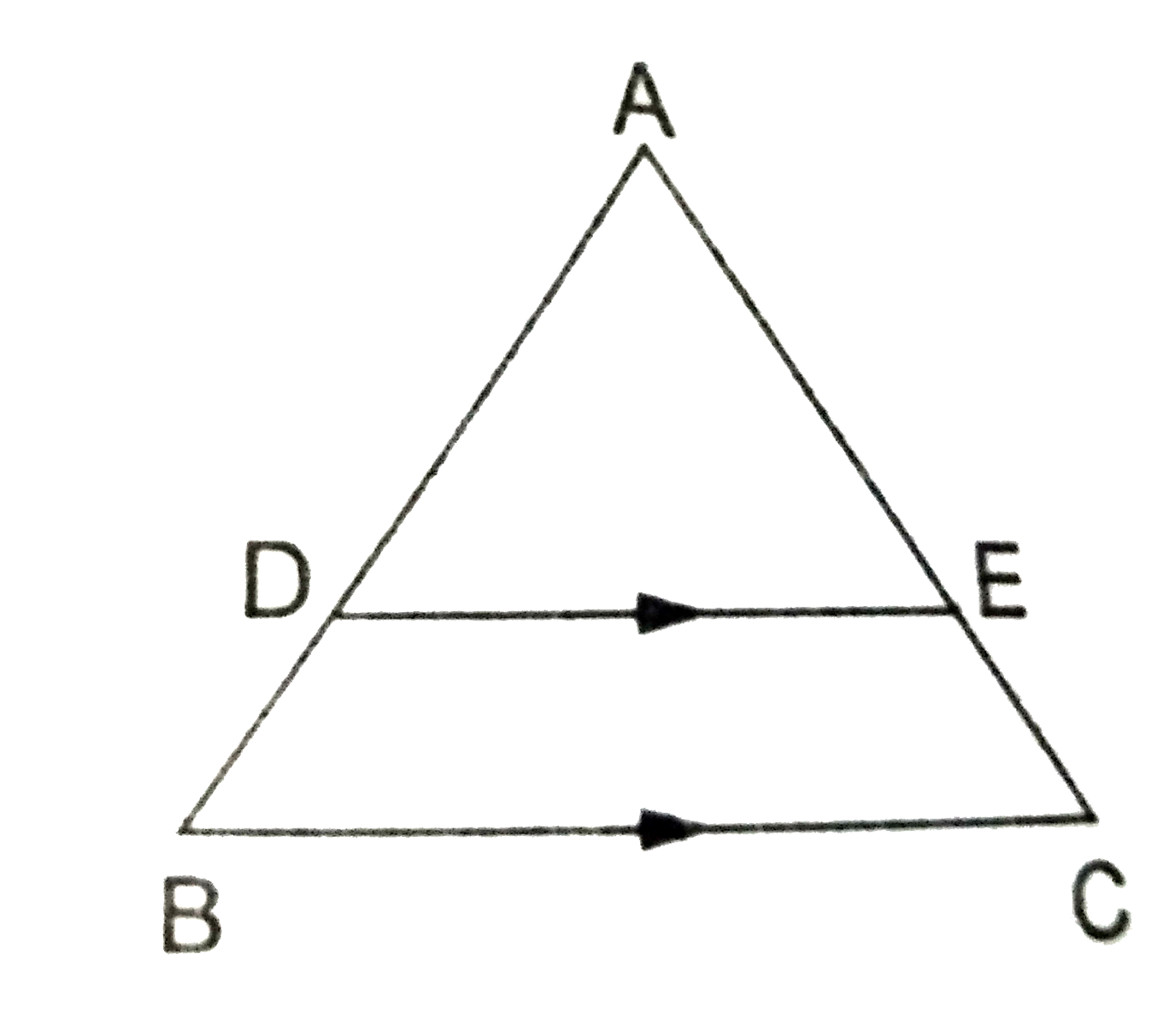
View SolutionABCD is a rectangle. The diagonals AC and BD intersect at O. If AB = 32 cm and AD = 24 cm, then what is OD equal to ?
View Solution

