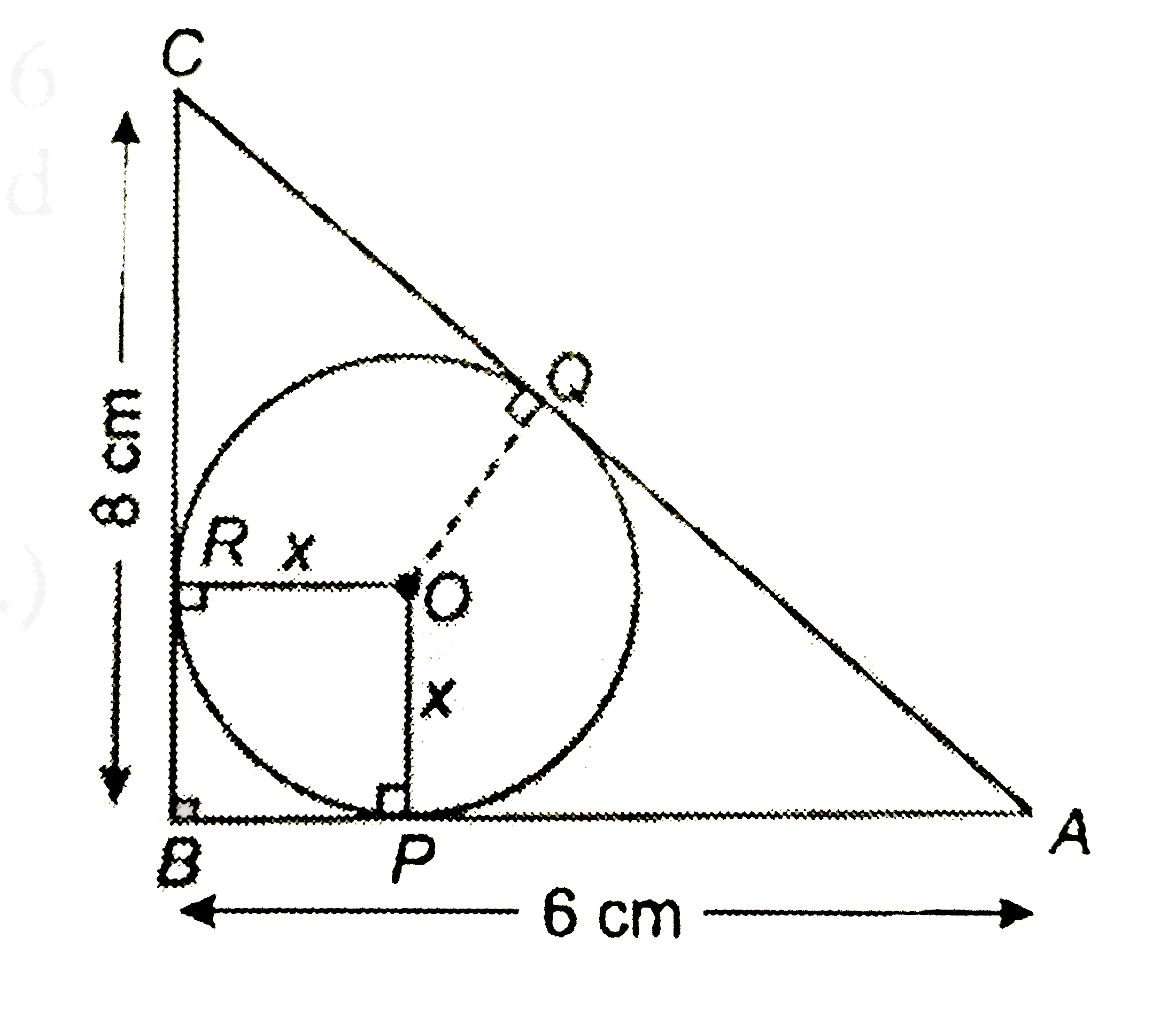
Given a right-angled $△ A B C$ . The lengths of the sides containing the right angle are 6 cm and 8 cm. A circle is inscribed in $△ A B C$ . Find the radius of the circle.

Video Solution

Text Solution

Verified by Experts

In $Δ A B C$ ,we have
$∠ B = 90^{\circ}, A B = 6 c m and B C = 8 c m$ .
A circle is inscribed in $Δ A B C$ . Let O be its centre and M,N and P be the points where it touches the sides AB,BC and CA respectively. Then,
$O M ⊥ A B, O N ⊥ B C, O P ⊥ C A$ .
Let r cm be the radius of the circle.
Then, $O M = O N = O P = r c m$
Now, $A B^{2} + B C^{2} = C A^{2}$ [ by Pythagora's theorem]
$\Rightarrow 6^{2} c m^{2} + 8^{2} c m^{2} = C A^{2} \Rightarrow C A = 10 c m$ .

Now, $a r (Δ A B C) = a r (Δ A O B) + a r (Δ B O C) + a r (Δ C O A)$
$\Rightarrow \frac{1}{2} \times A B \times B C (\frac{1}{2} \times A B \times O M) + (\frac{1}{2} \times B C \times O N) + (\frac{1}{2} \times C A \times P)$
$\Rightarrow \frac{1}{2} \times 6 \times 8 = (\frac{1}{2} \times 6 \times r) + (\frac{1}{2} \times 8 \times r) + (\frac{1}{2} \times 10 \times r)$
$\Rightarrow r = 2 \Rightarrow radius = 2 c m$

Updated on:21/07/2023