Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
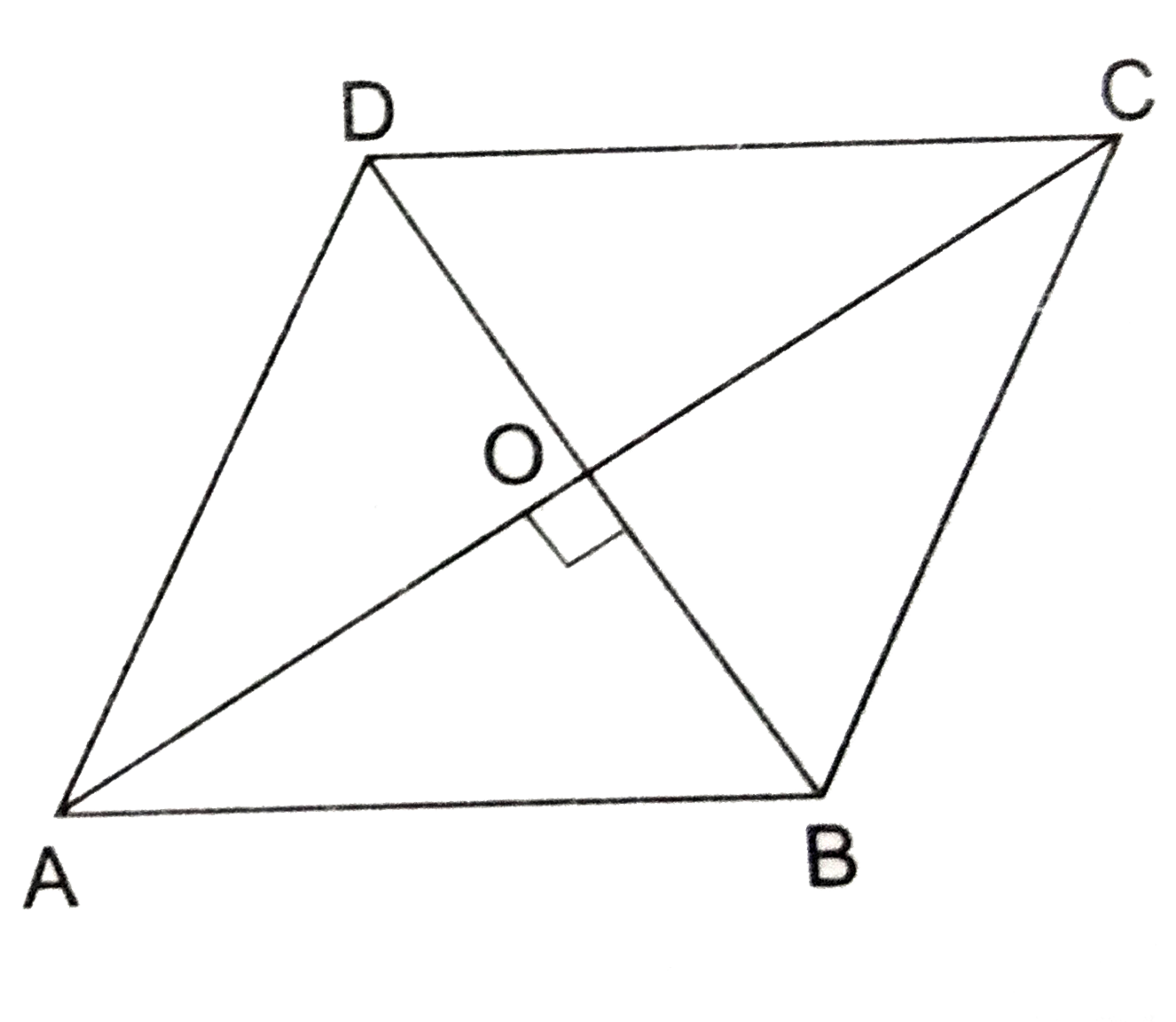
GIVEN A rhombus ABCD whose diagonals AC and BD intersect at O.
TO PROOVE (AB2+BC2+CD2+DA2)
=(AC2+BD2)
PROOF We know the bisect each other at right angles.
∴∠AOB=∠BOC=∠COD=∠DOA=90∘
AO=12ACandOB=12BD.
From right ΔAOB, we have
AB2=OA2+OB2
AB2=OA2+OB2 [ by Pythagora's theorem]
=(12AC)2+(12BD)2=14(AC2+BD2)
⇒4AB2=(AC2+BD2) ...(i)
Similarly, we have:
4BC2=(AC2+BD2) ....(ii)
4CD2=(AC2+BD2) ...(iii)
4DA2=(AC2+BD2) ...(iv)
On adding (i), (ii), (iii), and (iv) , we get
(AB2+BC2+CD2+DA2)=(AC2+BD2)
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:SOLVED EXAMPLE
Explore 4 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:EXERCISE 7 A
Explore 1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
Knowledge Check
Each side of a rhombus is 10 cm, the sum of square of its diagonal is
AA)20 cm2BB)200 cm2CC)400 cm2DD)100 cm2
Prove that the sum of squares of the diagonals of a parallelogram is equal to the sum of the squares of its sides.
View Solutionprove by vector method that the sum of the squares of the diagonals of a parallelogram is equal to the sum of the squares of its sides.
View SolutionProve by vector method that the sum of the square of the diagonals of a parallelogram is equal to the sum of the squares of its sides.
View SolutionProve that three times the sum of the squares of the sides of a triangle is equal to four times the sum of the squares of the medians of the triangle.
View SolutionProve that three times the sum of the squares of the sides of a triangle is equal to fourtimes the sum of the squares of the medians of the triangle.
View SolutionProve analytically that the sum of square of the diagonals of a rectangle is equal to the sum of squares of its sides.
View SolutionProve that three times the sum of the squares on the sides of a triangle is equal to four times the sum of the square on the medians of the triangle.
View Solution