$A B C$ is a right triangle right-angled at $C$ . Let $B C = a, C A = b, A B = c$ and let $p$ be the length of perpendicular from $C$ on $A B$ , prove that (i) $c p = a b$ (ii) $\frac{1}{p^{2}} = \frac{1}{a^{2}} + \frac{1}{b^{2}}$

Video Solution

Text Solution

Verified by Experts

(i) We have
$a r (Δ A B C) = \frac{1}{2} \times \frac{1}{2} \times A B \times C D = \frac{1}{2} c p$ [ taking BC as base]
$∴ \frac{1}{2} c p = \frac{1}{2} a b \Rightarrow c p = a p$ .

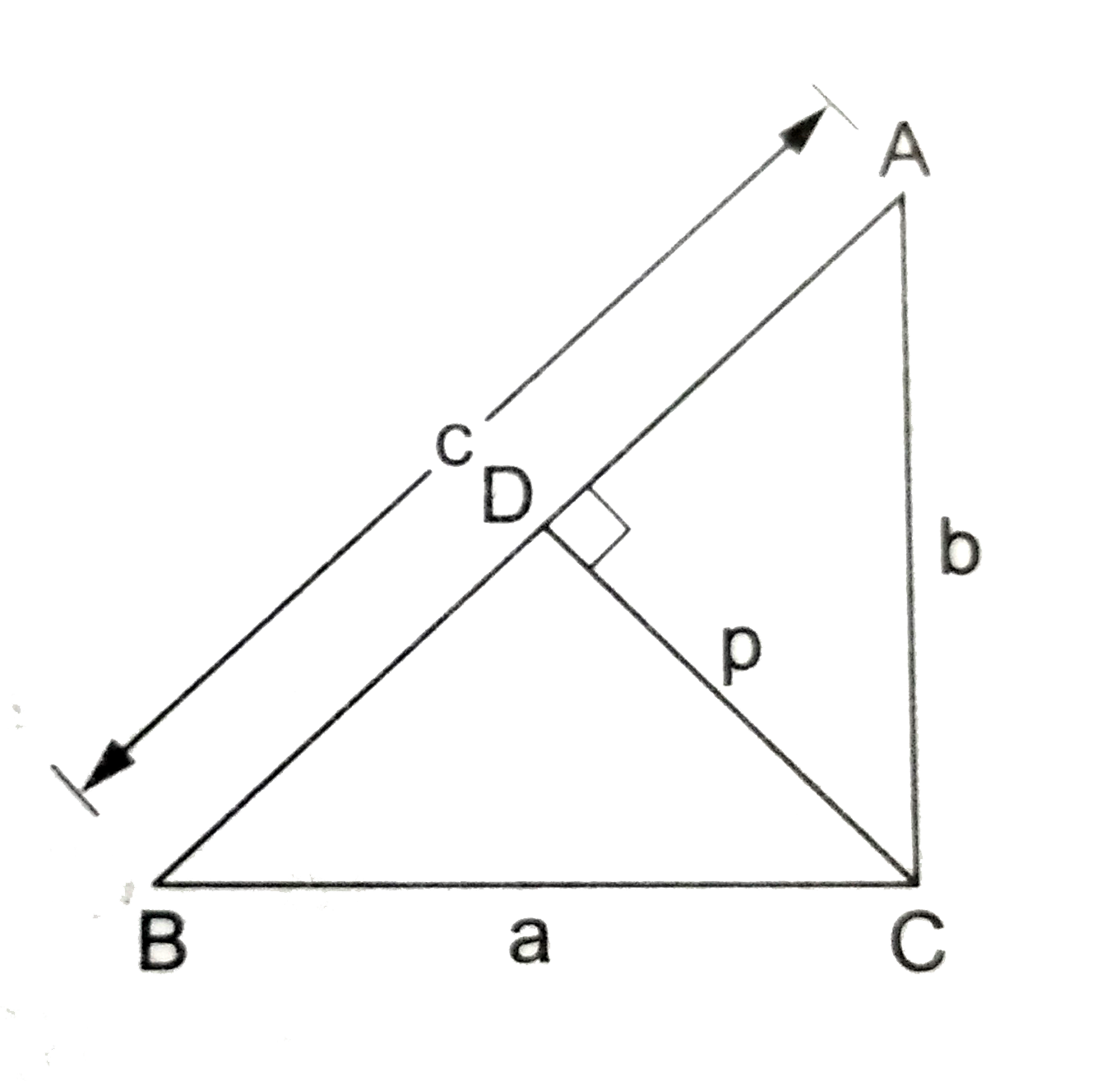
Hence, cp= ab.
$(i i) c p = a b \Rightarrow \frac{1}{p} = \frac{c}{a b}$
$∴ \frac{1}{p^{2}} = \frac{c^{2}}{a^{2} b^{2}} = \frac{b^{2} + a^{2}}{a^{2} b^{2}} [∴ A B^{2} = A C^{2} + B C^{2}]$
$= (\frac{b^{2}}{a^{2} b^{2}} + \frac{a^{2}}{a^{2} b^{2}}) = (\frac{1}{a^{2}} + \frac{1}{b^{2}})$
Hnece, $\frac{1}{p^{2}} = \frac{1}{a^{2} + \frac{1}{b^{2}}}$

|

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
ABC is a right angled triangle in which $∠ C = 90^{\circ}$ . If $B C = a, A B = c, C A = b$ and the length of perpendicular from C to AB be p. then, $\frac{1}{a^{2}} + \frac{1}{b^{2}} = ?$
A $\frac{1}{p}$
B $\frac{2}{p^{2}}$
C $\frac{1}{p^{2}}$
DNone of these

RS AGGARWAL-TRIANGLES-Test Yourself

Home
Ask Doubt
Profile