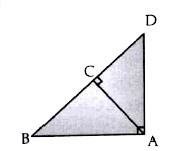
$Δ A B D$ is a right triangle, right-angled at A and $A C ⊥ B D$ . Prove that $A B^{2} = B C \times B D$ .

Video Solution

Text Solution

Verified by Experts

We know that:
If a perpendicular is drawn from the vertex of the right angle of triangle to the hypotenuse then the triangles on both sides hypotenuse then the triangles on both sides of the perpendicular are similar to the whole triangle and also to each other.

$∴ Δ A B C ~ Δ D B A$
$Δ A B C ~ Δ D A C$
$Δ D B A ~ Δ D A C$ .
$(i) Δ A B C ~ Δ D B A$
$\Rightarrow \frac{A B}{D B} = \frac{B C}{B A} \Rightarrow \frac{A B}{B D} = \frac{B C}{A B} \Rightarrow B C \cdot B D$ .
(ii) $Δ A B C ~ Δ D A C$
$\Rightarrow \frac{A C}{D C} = \frac{B C}{A C} \Rightarrow A C^{2} = B C \cdot D C$ .
$(i i i) Δ D B A ~ Δ D A C$
$\Rightarrow \frac{A D}{C D} = \frac{B D}{A D} \Rightarrow A D^{2} = B D \cdot C D$

Updated on:21/07/2023

|

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

Similar Questions

RS AGGARWAL-TRIANGLES-Test Yourself

Home
Ask Doubt
Profile