In a rhombus of side 10 cm, one of the diagonals is 12 cm long. The length of the second diagonals is

Video Solution

Text Solution

Verified by Experts

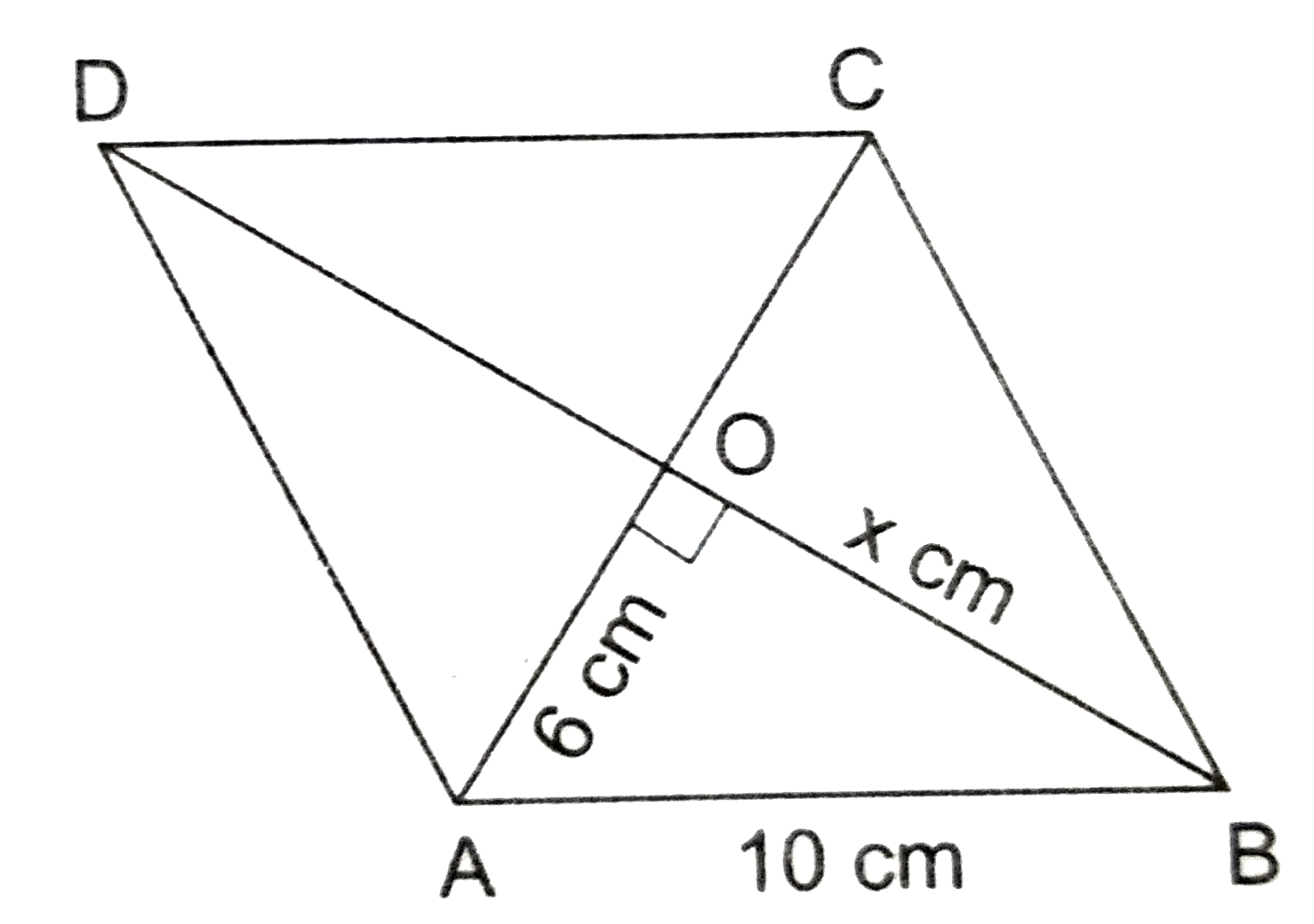
Let ABCD be the given rhomus whose diagonals intersect at O. then, $A B = 10 c m$
Let $A C = 12 c m and B D = 2 x c m$ .
We know that the diagonals of a rhombus bisect each other at right angles.
$∴ O A = \frac{1}{2} A C = 6 c m, O B = \frac{1}{2} B D = x c m, and ∠ A O B = 90^{\circ}$
From right $Δ A O B$ , we have
$A B^{2} = O A^{2} + O B^{2}$
$\Rightarrow O B^{2} = A B^{2} - O A^{2}$
$= {{(10)}^{2} - {(6)}^{2}} c m^{2} = (100 - 36) c m^{2} = 64 c m^{2}$
$\Rightarrow x^{2} = 64 \Rightarrow x = \sqrt{64} = 8$
$∴ O B = 8 c m$
$∴ B D = 2 \times O B = 2 \times 8 c m = 16 c m$
Hence, the length of the second diagonal is 16cm.

Updated on:21/07/2023

The length of a side of a rhombus is 10 m and one of its diagonal is 12 m. The length of the other diagonal is :
A15 m
B18 m
C16 m
Dcan't be determined
The perimeter of a rhombus is 40 cm. If one of the diagonals be 12 cm long, what ia the length of the other diagonal ?
A12 cm
B $\sqrt{136} c m$
C16 cm
D $\sqrt{44} c m$
The length of a side of a rhombus is 10 m and one of its diagonal is 12 m. The length of the other diagonal is :
A15 m
B18 m
C16 m
Dcan't be determined