A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
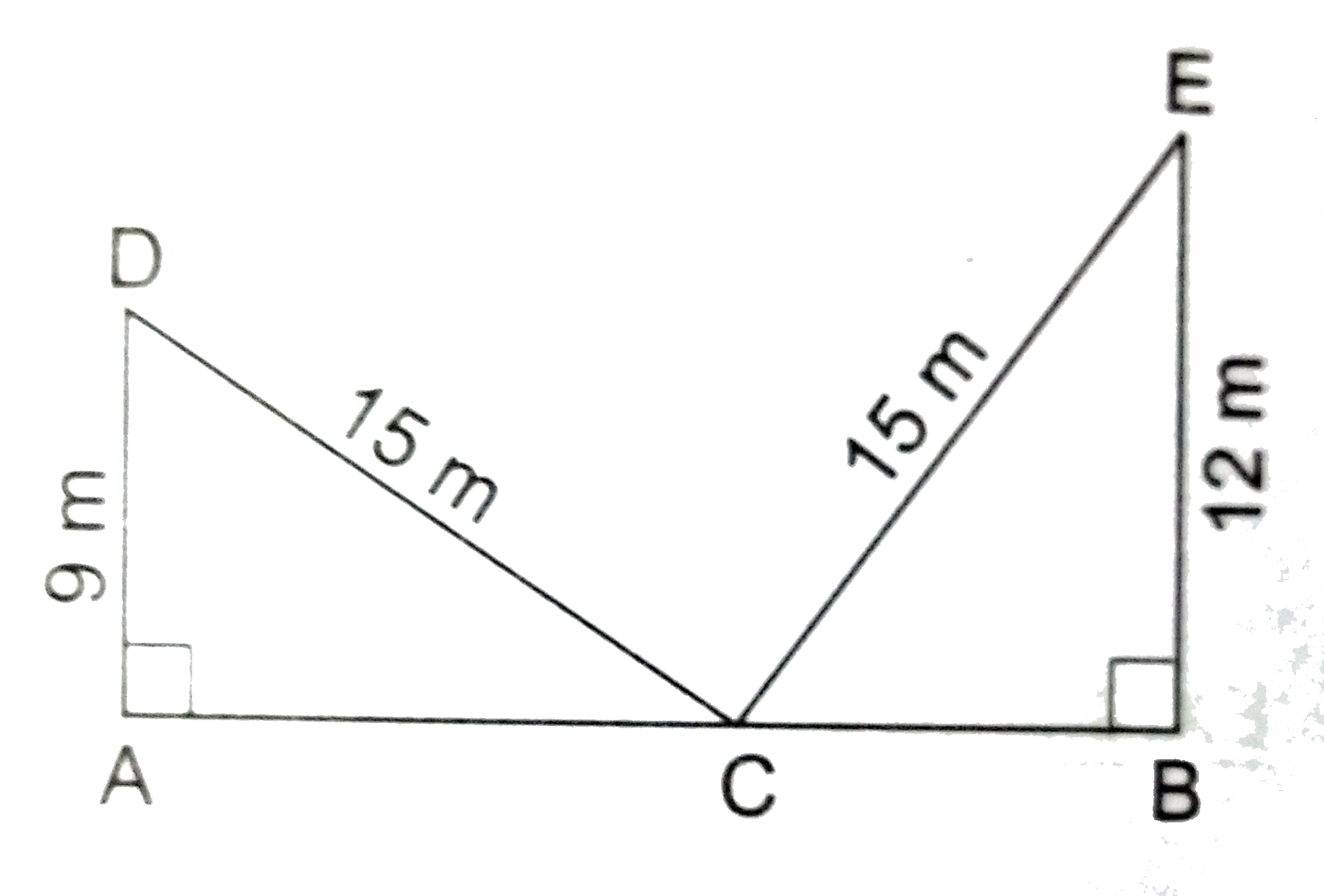
Let AB be the street and let c be the foot of the ladde. Let D and E be right windows such that AD=9mandBE=12m.
Then CDandCE are the two position of the ladder.
Clearly, ∠CAD=90∘,∠CBE=90∘
andCD=CE=15m
From right ΔCAD , we have
CD2=AC2+AD2[ by Pythagora's theorem]
⇒AC2=CD2−AD2=[(15)2−(9)2]m2=(225−81)m2=144m2
⇒AC=√144m=12m.
From right ΔCBE, we have
CE2=CB2+BE2 [ by Pythagora's theorem]
⇒CB2=CE2−BE2=[(15)2−12]m2=(225−144)m2=81m2
⇒CB=√81m=9
Width of the street =AC+CB=12m+9m21m.
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:SOLVED EXAMPLE
Explore 4 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:EXERCISE 7 A
Explore 1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
A ladder 15 m long reaches a window which is 9 m above the ground on one side of a street. Keeping its foot at the some point, the ladder is turned to other side of the street to reach a window 12 m high. Find the width of the street.
View SolutionA ladder 13 m long reaches a window which is 12 m above the ground on side of a street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 5m high, then the width of the street is:
View SolutionA ladder reachs a window which is 15 metres above the ground on one side of the steet. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 8 metres high. Find the width of the street, if the ladder is 13 meters.
View SolutionProve that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Using the above, solve the following: A ladder reaches a window which is 12 m above the ground on one side of the street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 9m high. Find the width of the street if the length of the ladder is 15 m
View SolutionA ladder of 17 ft. length reaches a window which is 15 ft. above the ground on one side of the street. Keeping its foot at the same point the ladder is turned to the other side of the street and now it reaches a window 8 ft. high. What is the width of the street ?
View SolutionA ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from the base of the wall.
View SolutionA ladder 10m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
View SolutionA ladder 10m long reaches a window 8m above the ground. Find the distance of foot of the ladder from base of the wall.
View SolutionA ladder 25 m long reaches a window of a building 20 m above the ground. Determine the distance of the foot of the ladder from the building.
View SolutionA ladder 25m long reaches a window of a building 20m above the ground. Determine the distance of the foot of the ladder from the building.
View Solution

