In the adjoining figure, S and T are points on the sides PQ and PR respectively of ΔPQR such that PT=2cm,TR=4cmandST is parallel to QR. Find the ratio of the ares ofΔPSTandΔPQR.
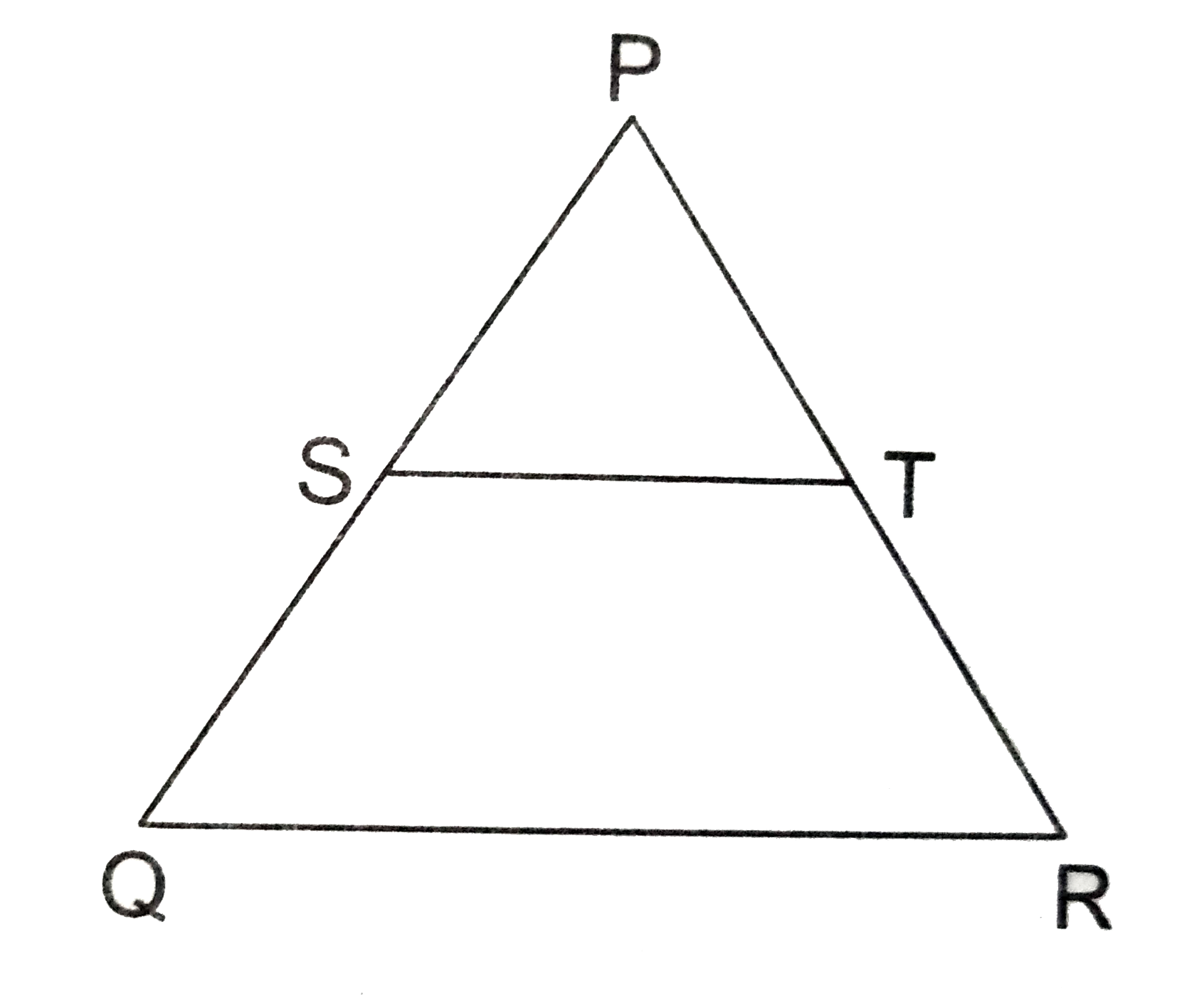
ST∣∣OQ (given)
∴∠PST=∠PQR[ corresponding angles] ltbr and∠PTS=∠PRQ [ corresponding angles.]
And So, ΔPST~ΔPQR[ by AA- similarity]
∴ar(ΔPST)ar(ΔPQR)=PT2PR2=PT2(Pt+TR)2
=22(2+4)2=436=19
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:SOLVED EXAMPLE
Explore 4 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:EXERCISE 7 A
Explore 1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
S and T are points on the sides PQ and PR, respectively of ΔPQR, such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ΔPST and ΔPQR.
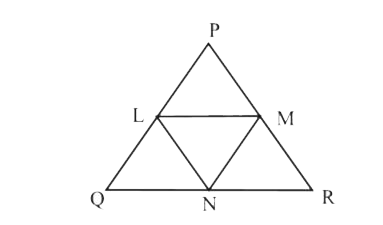
View SolutionIn the given figure L, M and N are mid point of the sides PQ, PR and QR respectively of ΔPQR. If PQ = 4.4 cm, QR = 5.6 cm and PR = 4.8 cm then find the perimeter of ΔLMN.
View Solution
Knowledge Check
In the triangle PQR below, - S and T are 2 points on the sides RP and RQ respectively such that ST is parallel to PQ.
- The ratio of RT to TQ is 1:2.
The area of ΔRST = 100 sq. units.
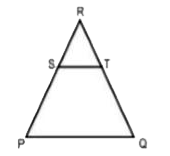
What is the area of PQTS?A200 sq. unitsB300 sq. unitsC600 sq. unitsD800 sq. unitsIn △PQR L and M are two points on the sides PQ and PR respectively such that LMII QR. If PL = 2cm, LQ = 6 cm and PM= 1.5 cm, then MR (in cm) is
A0.5B4.5C9D8In ΔPQR, point S and T are on sides Pr and PQ such that ∠PQR=∠PST. If PT= 5 cm., PS = 3 cm. And TQ = 3 cm. then length of SR will be-
A5 cmB6 cmC313cmD413cm
S and T are points on sides PR and QR of ΔPQRsuch that ∠P=∠RTS. Show that ΔRPQ~ΔRTS.
View SolutionS and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS Show that ΔRPQ~ΔRTS
View SolutionIn the given figure, S and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS. Show that ΔRPQ~ΔRTS.
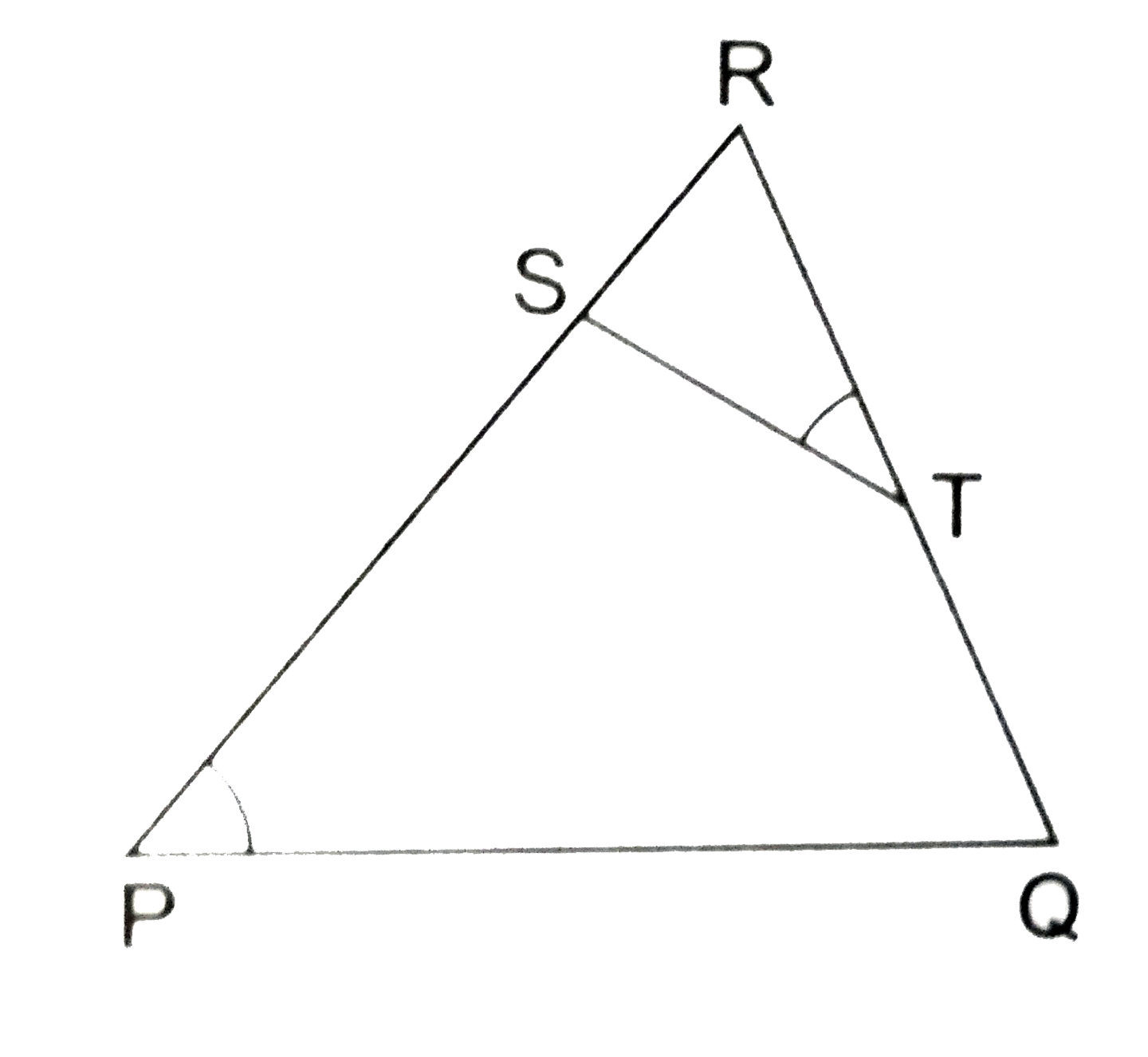
View SolutionIn ΔPQR, point S and T are on sides Pr and PQ such that ∠PQR=∠PST. If PT= 5 cm., PS = 3 cm. And TQ = 3 cm. then length of SR will be-
View SolutionE and F are points on the sides PQ and PR respectively of a ΔPQR. Show that Ef||QR. If PQ = 1.28 cm,PR= 2.56 cm,PE = 0.18 cm and PF= 0.36 cm.
View Solution

