Through the mid-point M of the side CD of a parallelogram ABCD , the line BM is drawn intersecting AC at LandAD produced at E . Prove that EL=2BL.
A∣∣gmABCDandM is the midpoint of CD. Line MB is drawn, intersecting AC in L and AD production in E.
TO PROVE EL=2BL
PROOF In ΔBMCandΔEMD, we have
∠1∠2 (vert opp.∠)
MC=MD [ M is the midpoint of CD]
∠BCM=∠EDM [ alternate interior ∠]
∴∠MBC≅ΔEMD
∴BC=DE
But, BC=AD [ opposite sides of a ||gm]
∴BC=AD=DE⇒AE=(AD+DE)=2BC ....(i)
Now, in ΔAELandΔCBL, we have
∠6=∠5 (vert. opp. ∠]
∠3=∠4 [ alternate interior ∠]
∴ΔAEl~ΔCBL [ AA- similarity]
⇒ELBL=AEBC=2BCBC=2 [ using (i)]
⇒EL=2BL.
Hence, EL= 2BL.

Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:SOLVED EXAMPLE
Explore 4 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:EXERCISE 7 A
Explore 1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
Through the mid-point M of the side CD of a parallelogram ABCD , the line BM is drawn intersecting AC at LandAD produced at E . Prove that EL=2BL.
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A line through B parallel to PD meets DC at Q and AD produced at R. Prove that: AR=2BC (ii) BR=2 BQ
View SolutionThe diagonals of a parallelogram ABCD intersect at OA line through O intersects AB at XandDC at Y Prove that OX=OY
View SolutionIn Figure, X, Y are the mid-points of opposite sides AB and DC of a parallelogram ABCD.AY and DX are joined intersecting in P;CX and BY are joined intersecting in Q . Show that AXCY is a parallelogram (ii) DXBY is a parallelogram quadrilateral PXQY is a parallelogram
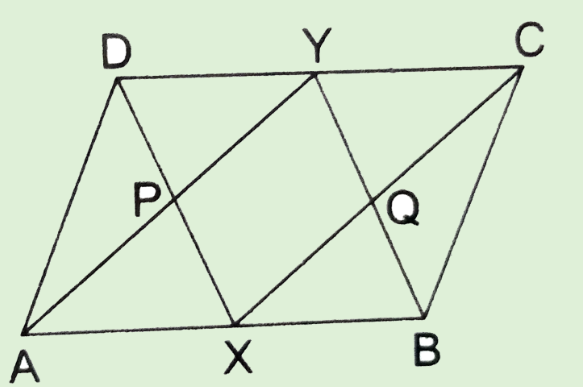
View SolutionE,F,G,H are respectively, the mid-points of the sides AB,BC,CD and DA of parallelogram ABCD . Show that the quadrilateral EFGH is a parallelogram and that its area is half the area of the parallelogram, ABCD. GIVEN : A quadrilateral ABCD in which L,F,G,H are respectively the mid-points of the sides AB,BC,CD and DA. TO PROVE : (i) Quadrilateral EFGH is a parallelogram ar(^(gm)EFGH)=12ar(^(gm)ABCD) CONSTRUCTION : Join AC and HF
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
View SolutionABCD is a parallelogram. AD is a produced to E so that DE=DC and EC produced meets AB produced in F. Prove that BF=BC.
View SolutionABCD is a cyclic quadrilateral. ABandDC are produced to meet in E. Prove that EBC−EDA.
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ

View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(ADF)=ar(DCE).
View Solution
