In a △ABC P and Q are points on AB and AC respectively and PQ||BC. Prove that the median AD bisects PQ.
Video Solution
Text Solution
GIVEN A ΔABC in which P and Q are points on AB and AC respectively such that PQ∣∣BCandAD is the median, cutting PQ at E.
TO PROVE PE=EQ.
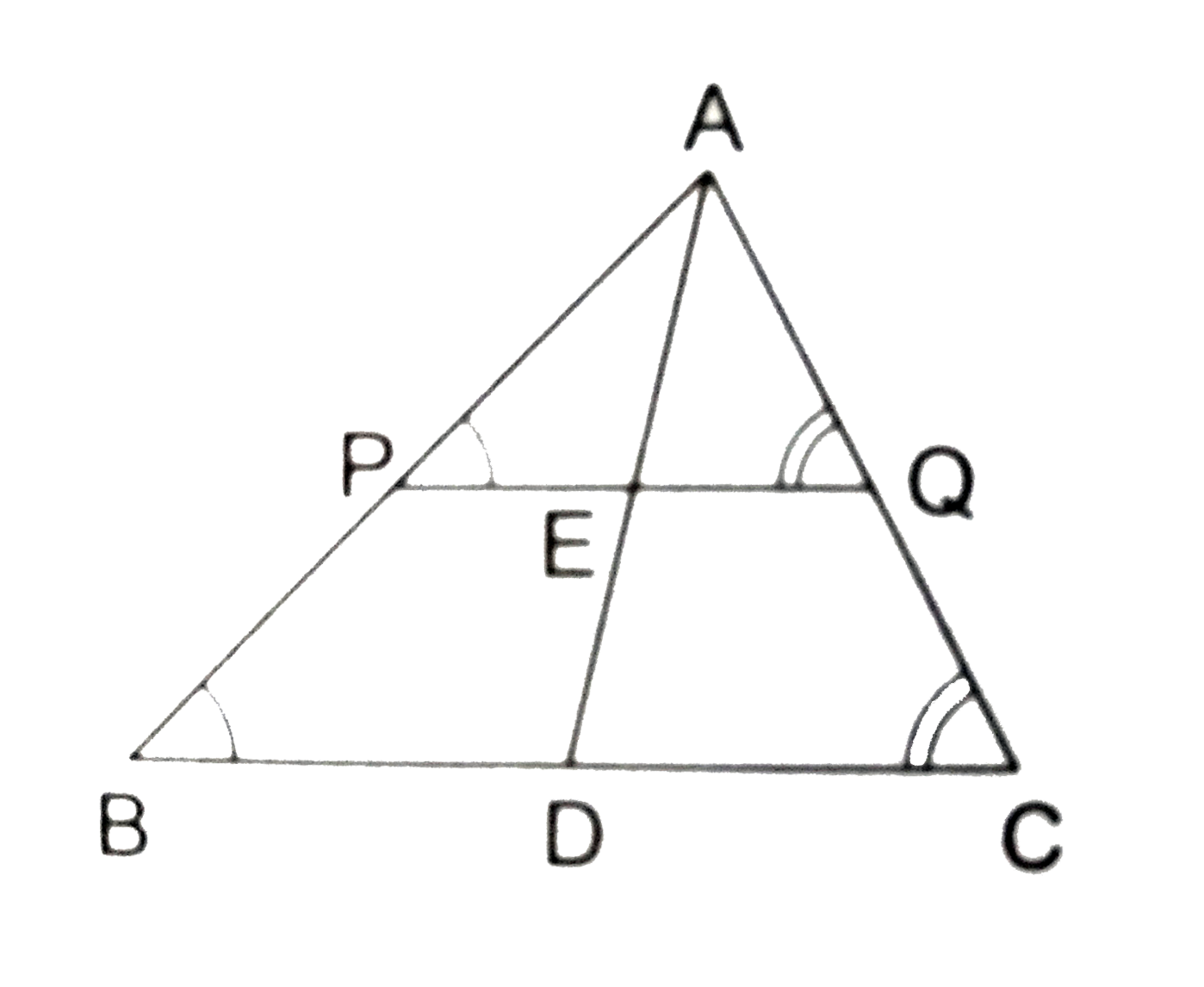
PROOF In ΔAPEandΔABD, we have
∠PAE=∠BAD [ common]
∠APE=∠ABD [ corrsponding ∠]
∴ΔAPE~ΔABD [ buy AA- similarity]
But, in similar triangles, the corresponding sides are proportional.
∴AEAD=PEBD
In ΔAEQandΔADC, we have
∠QAE=∠CAD [ common]
∠AQE=∠ACD [ corresponding angles]
∴ΔAEQ~ΔADC [ by AA- similarity]
But, in similar triangles, the correponding sides are proportional.
∴AEAD=EQDC ....(ii)
From (i) and (ii), we get PEBD=EQDC [each equal toAEAD]
But, BD=DC [∴ADis the median]
∴PE=EQ
|
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Knowledge Check
In a rectangle ABCD, P,Q are the mid-points of BC and AD respectively and R is any point on PQ, then ΔARB equals :
A1/2(□ABCD)B1/3(□ABCD)C1/4(□ABCD)Dnone of theseIn a rectangle ABCD, P,Q are the mid-points of BC and AD respectively and R is any point on PQ, then ΔARB equals :
A12(□ABCD)B13(□ABCD)C14(□ABCD)Dnone of theseABC is an equilateral triangle. P and Q are two points on ¯¯¯¯¯¯AB and ¯¯¯¯¯¯AC respectively such that ¯¯¯¯¯¯PQ∣∣¯¯¯¯¯¯BC. If ¯¯¯¯¯¯PQ=5cm, then area of ΔAPQ is :
A254 sq. cmB25√3 sq. cmC25√34 sq. cmD25√3 sq. cm
If DE||BC in △ABC where D and E are points on AB and AC respectively. If ADDB=815 and EC = 3.5 cm , find AE.
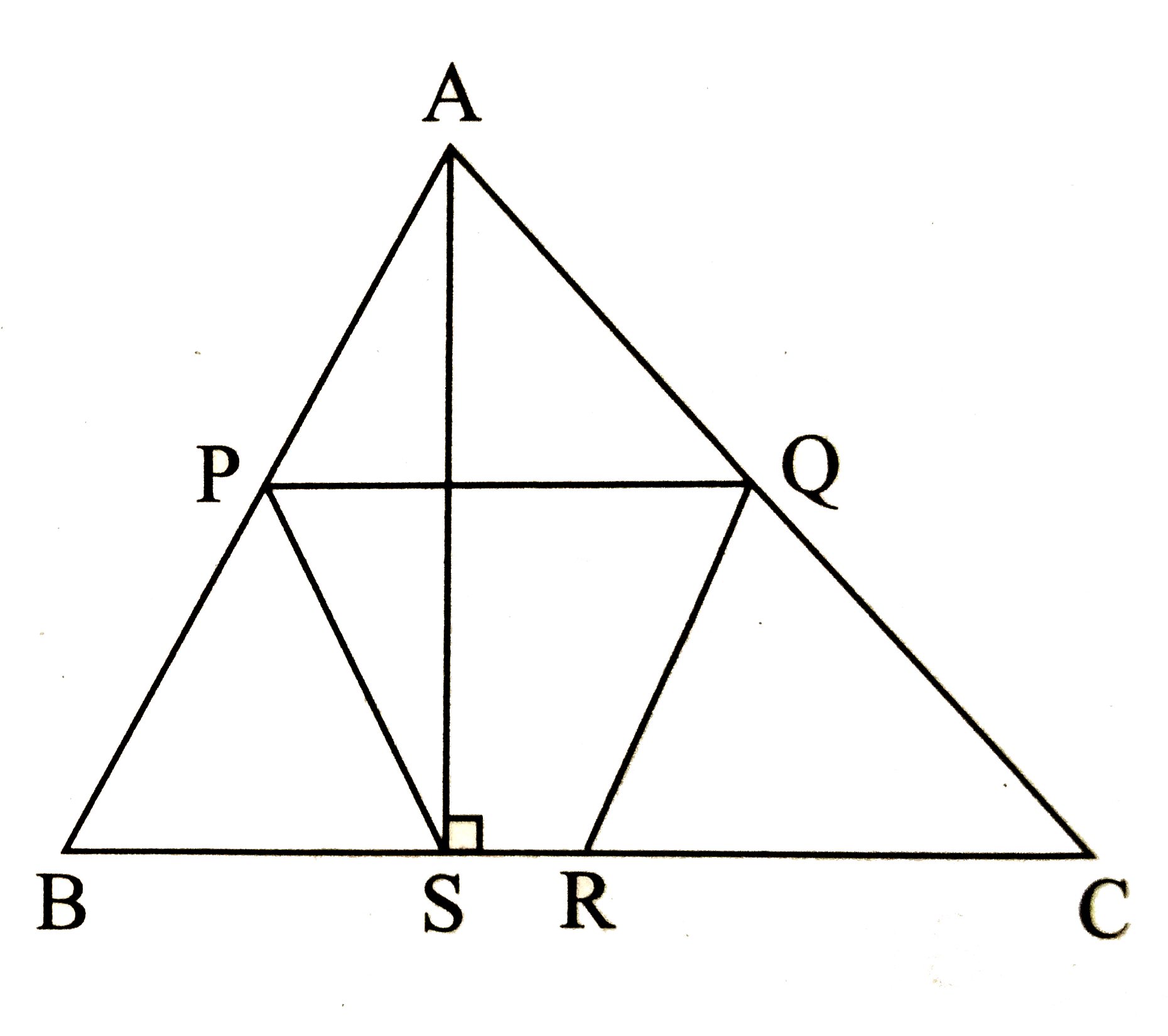
View SolutionIn ΔABC, P,Q and R are midpoints of sides AB,AC and BC respectively. Seg AS⊥BC and PQ || BR side BC. Prove that □ PQRS is a cyclic quadrilateral.
View SolutionIf P and Q are points on the sides AB and AC respeactively of △ABC, if PQ||BC,l AP= 2 cm , AB = 6 cm and AC= 9 cm find AQ.
View SolutionIn ΔABC, PQ is parallel to BC, while P and Q are at AB and AC respectively. If AB = 3AP, then what is the ratio of areas of triangles ΔAPQ and ΔABC.
View SolutionIn a ΔABC,AB=AC,PandQ are points on AC and AB respectively such that CB=BP=PQ=QA. if ∠AQP=θ, then tan2θ is a root of the equation
View Solution
