Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that OAOC=OBOD
GIVEN A trapezium. ABCD in which AB∣∣DC. The diagonals AC and BD intersect at O.
TO PROOVE OAOC=OBOD
PROOF In ΔOABandΔOCD, we have
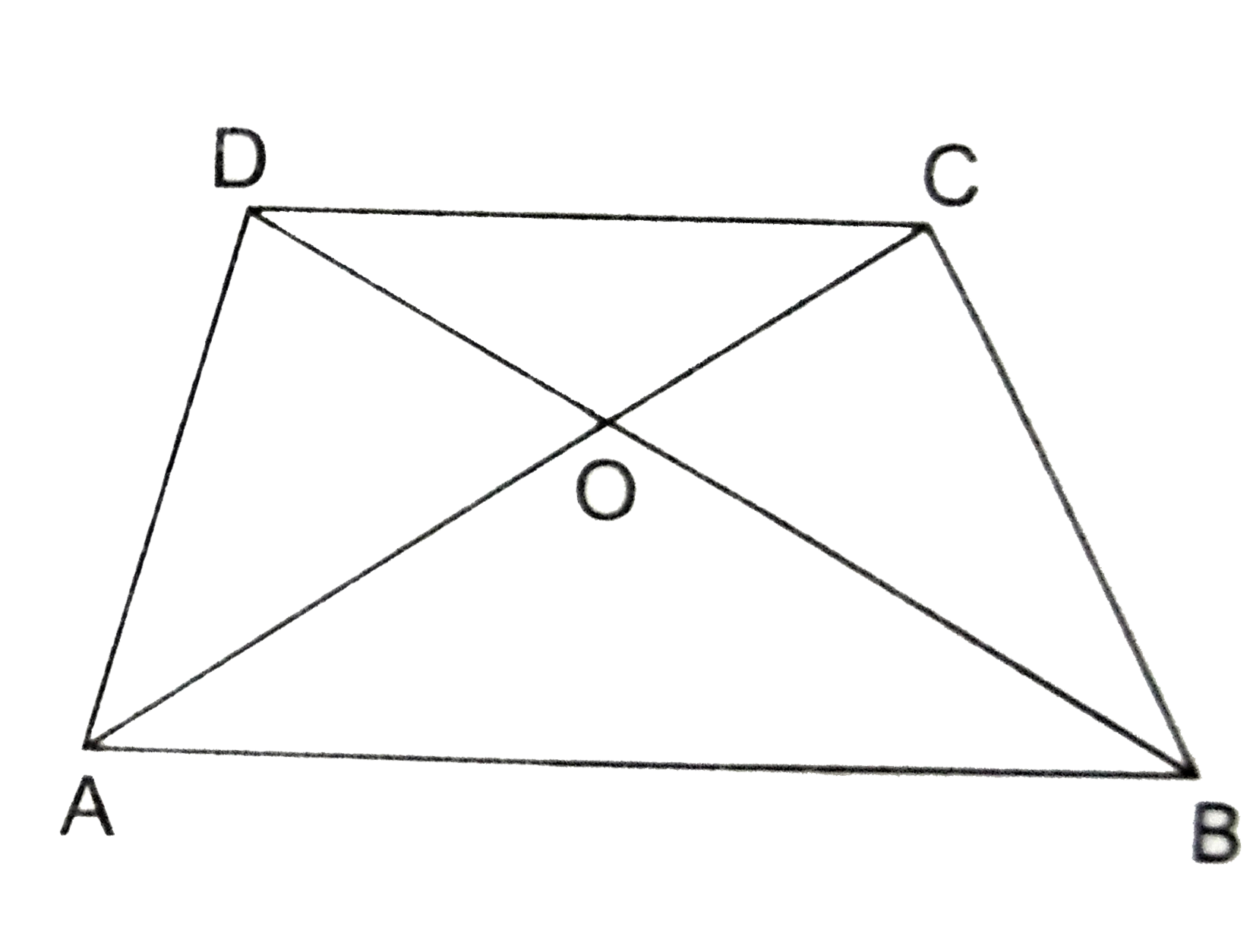
∠OAB=∠OCD [ alternate angels, since AB∣∣DC]
and ∠OAB=∠ODC [ alternative angles since AB∣∣DC]
∴ΔOAB~ΔOCD [ by AA- similarity]
And so, OAOC=OBOD
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that OAOC=OBOD
View SolutionDiagonals AC and BD of a trapezium ABCD with ABDC intersect each other at the point O . Using similarity criterion for two triangles, show that OAOC=OBOD .
View Solution
Knowledge Check
Diagonals of a Trapezium ΔBCD with AB || CD intersect each other at the point O. If AB = 2CD, then the ratio of the areas of ΔAOB and ΔCOD is
A4:1B1:16C1:4D16:1The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, then ∠DBC is equal to
A24∘B86∘C38∘D32∘The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, then ∠DBC is equal to
A24∘B86∘C38∘D32∘
Diagonals ACandBD of a trapezium ABCD with AB∣∣DC intersect each other at O . Prove that ar(AOD)=ar(BOC) .
View SolutionDiagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar(ΔAOD) = ar(ΔBOC).
View SolutionDiagonals AC and BD of a trapezium ABCD with ABCD intersect each where at O. Prove that ar (AOD)=ar(BOC).
View SolutionDiagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
View Solutionif ABCD is a trapezium, ACandBD are the diagonals intersecting each other at point Q. then AC:BD=
View Solution
