If two triangles are similar; prove that the ratio of the corresponding sides is same as the ratio of corresponding medians.
Video Solution
Text Solution
GIVEN ΔABCandΔPQR in which BC=a,CA=b,AB=candQR=o,RP=q,PQ=r. Also, ΔABC~ΔPQR.
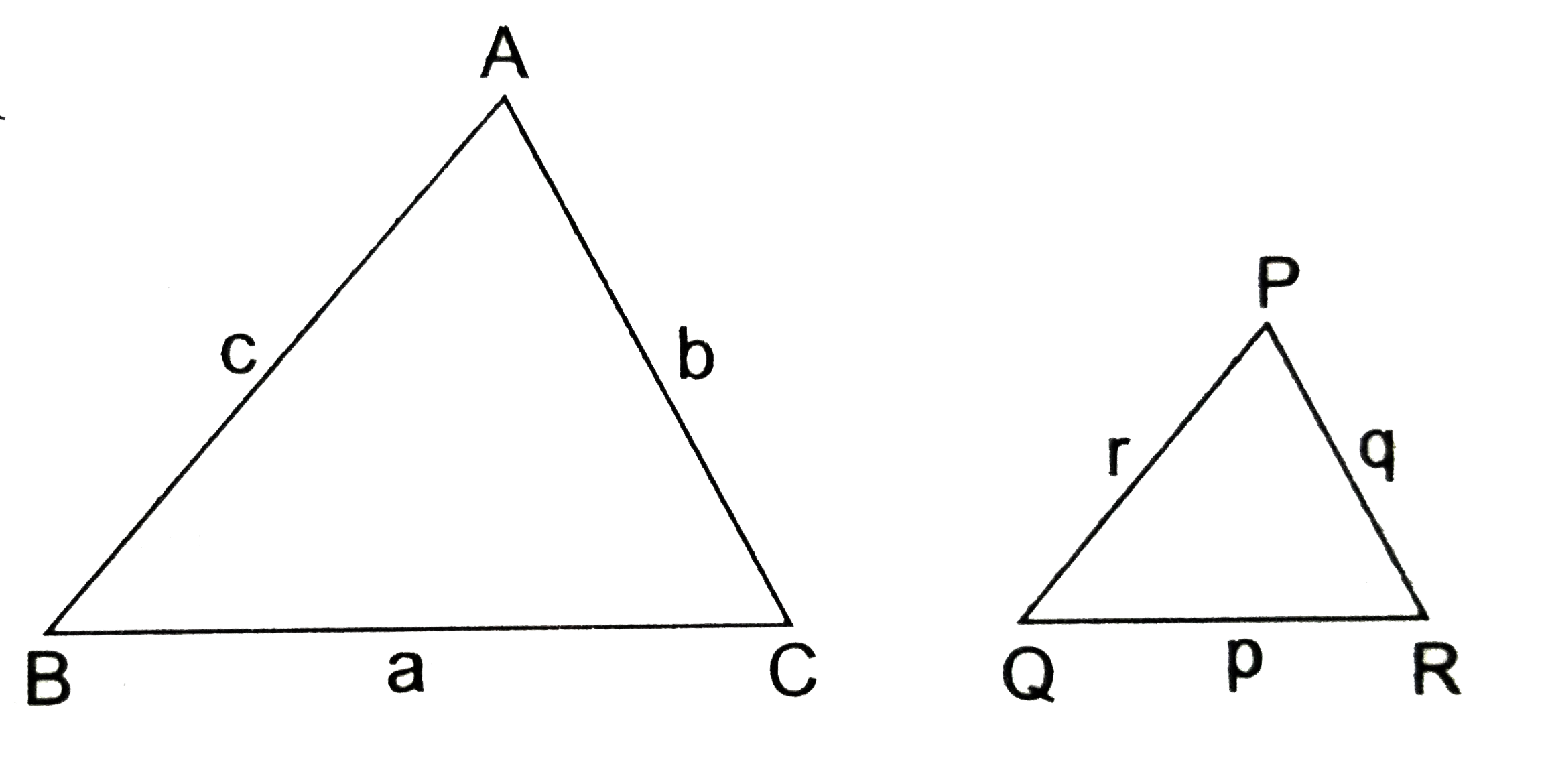
TO PROVE ap=bq=cr=a+b+cp+q+r
PROOF Since ΔABCandΔPQR are similar, therefore, their corresponding sides are proportional.
∴ap=bq=cr=k(say) ....(i)
∴perimete ofΔABCperimeter ofΔPQR=a+b+cp+q+r=kp+kq+krp+q+r=k(p+q+r)(p+q+r)=k ...(ii)
From (i) and (ii), we get
ap=bq=cr=a+b+cp+q+r=perimete of ΔABCperimeter of ΔPQR [ each equal to k.]
|
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:SOLVED EXAMPLE
Explore 4 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:EXERCISE 7 A
Explore 1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
Knowledge Check
If the angles of a triangle are in the ratio 1:2:3,the corresponding sides are in the ratio
A2:3:1B√3:2:1C2:√3:1D1:√3:2If area of two similar triangle are equal then ratio of their corresponding altitude is.
A1:1B1:√2C1:2DCannot be determinedIf the angles of a triangle ABC are in the ratio 1:2:3. then the corresponding sides are in the ratio ?
A1:2:3B3:2:1C1:√3:2D1:√3:√2
Prove that the ratio of the perimeters of two similar triangles is the same as the ratio of their corresponding sides.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the ratio of squares of their corresponding medians.
View SolutionThe areas of two similar triangles are 81 cm2 and 49 cm2 respectively. Find the ratio of their corresponding heights. What is the ratio of their corresponding medians?
View SolutionTwo triangles are similar if their corresponding sides are ………….
View SolutionArea of two similar triangles are in the ratio of 5:3 then the ratio of their corresponding sides is :
View Solution