ABCD is a trapezium with AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB. Show thatAEED=BFFC.
GIVEN A trap. ABCD in which AB∣∣CD.EandF are points on AD and BC respectively such that EF||AB.
Tom PROVE AEED=BFFC
CONSTRUCTION Join AC, interescting EF at G.
PROOF EF||ABandAB||DC⇒EF∣∣DC.
Now, in ΔABC,EG∣∣DC.
∴AEED=AGGC ..(i) [ by Thale's theorem]
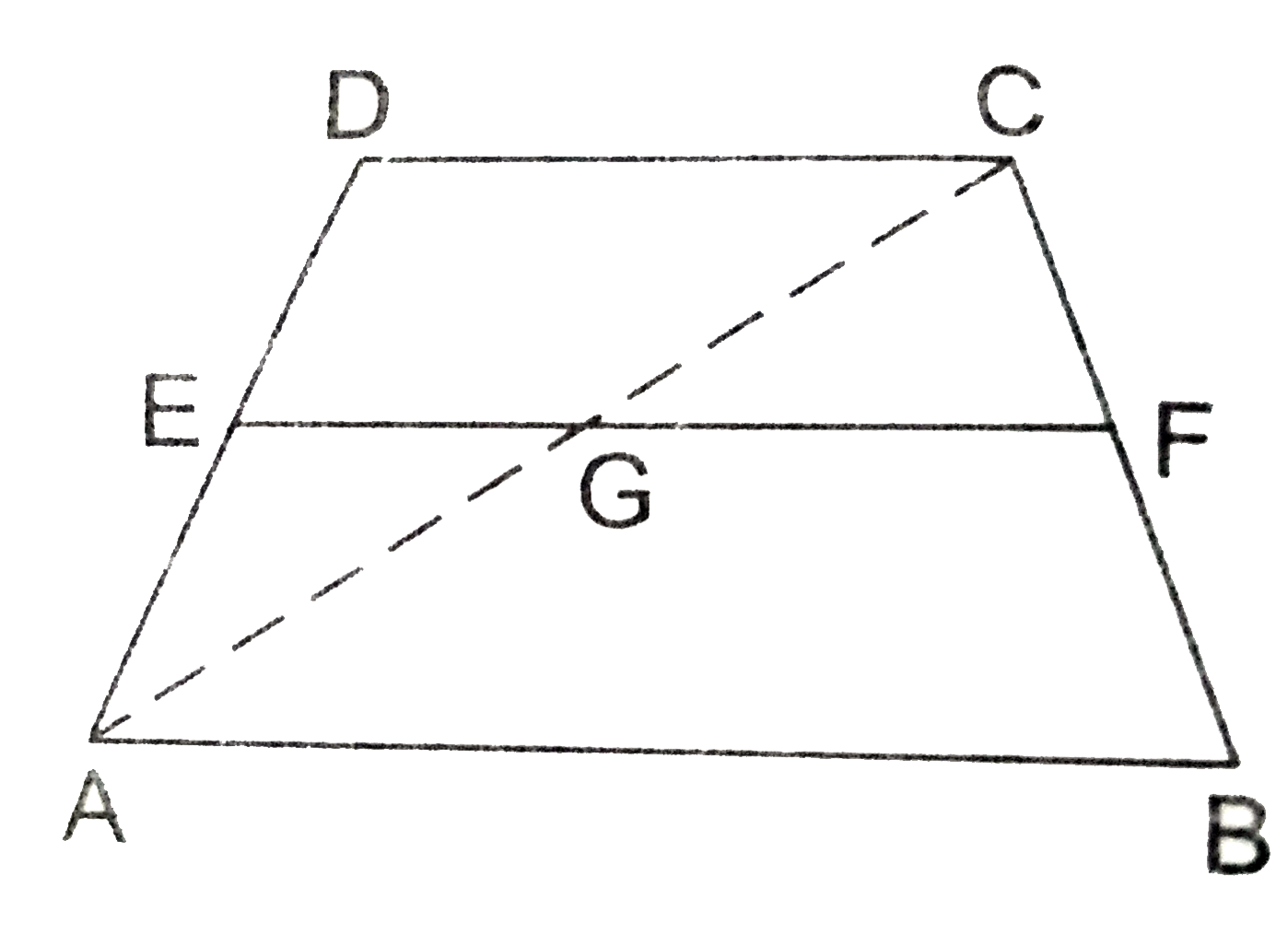
Similarly, in ΔCAB,GF∣∣AB.
∴CGGA=CFFB [ by Thale's theorem]
⇒AGGC=BFFC ...(i)
From (i) and (ii), we get
AEED=BFFC
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Knowledge Check
ABCD is a trapizium with AB∣∣DC. E and F are points on non - parallel sides AD and BC respecitively such that EF∣∣AB, If AE = 3cm, ED = 4.8 cm, BF = 1.5 cm, then the value of CF is :
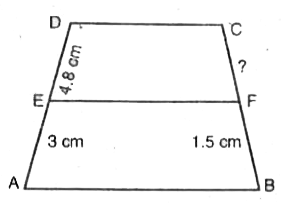 A4.5 cmB2.4 cmC6.0 cmDNone of these
A4.5 cmB2.4 cmC6.0 cmDNone of theseABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :
 A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2
A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2In a ΔABC,D,E,F are the mid -points of the sides BC, CA and AB respectively, the vector AD is equal to
A−−→BE+−−→CFB−−→BE−−−→CFC−−→CF−−−→BED−−−→BE−−−→CF
ABCD is a trapezium with parallel sides AB=a and DC=b. If EandF are mid-points of non-parallel sides ADandBC respectively, then the ratio of areas of quadrilaterals ABFEandEFCD is:
(a) a:b
(b) (a+3b):(3a+b)
(c) (3a+b):(a+3b)
(d) (3a+b):(3a+b)
View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

View SolutionIn Figure, ABC is a triangle in which AB=AC. Point DandE are points onthe sides ABandAC respectively such that AD=AE. Show that the points B,C,EandD are concyclic.
View SolutionD and E are points on the sides AB and AC respectively such that AB=3.6 cm and AD=1.4 AC=7.2 and AE=1.8. Show that DE is parallel to BC
View SolutionD and E are points on the sides AB and AC respectively such that AB=3.6 cm and AD=1.4 AC=7.2 and AE=1.8. Show that DE is parallel to BC
View Solution
