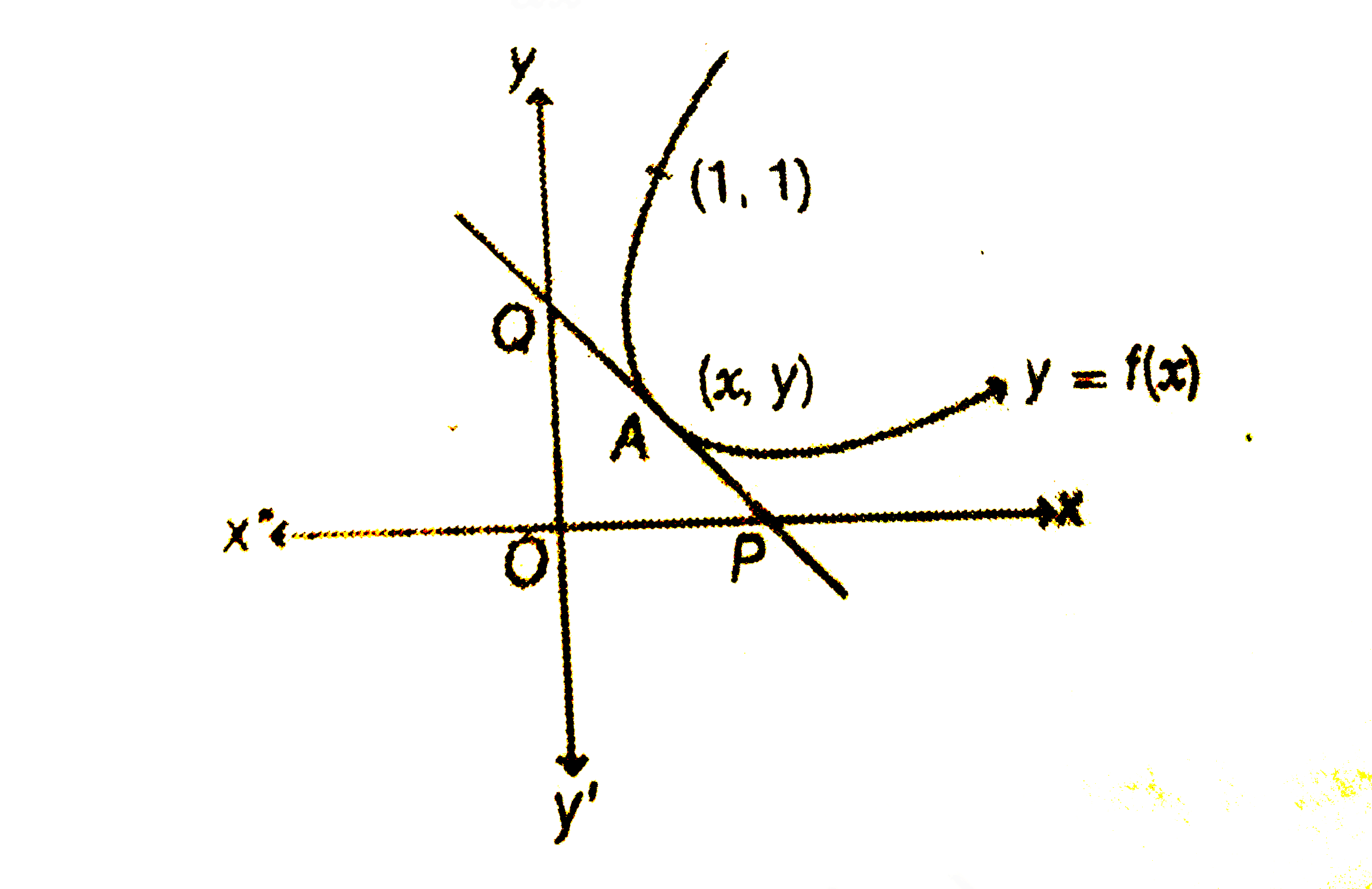
Let y=f(x) be a curve passing through (1,1) such that the triangle formed by the coordinate axes and the tangent at any point of the curve lies in the first quadrant and has area 2. Form the differential equation and determine all such possible curves.
The correct Answer is:Differential Equation: d2ydx2=0,x2dydx+1=0
curvers: x+y=2,xy=1
Equation of tangent to the curve y= f(x) at point
A(x,y)isY−y=dydx(X−x)
whose, x-intercept (x−y⋅dxdy,0)
y-intercept (0,y−xdydx)
Given, ΔOPQ=2
⇒12(x−ydxdy)(y−xdydx)=2
⇒(x−y1p)(y−xp)=4,wherep=dydx
⇒p2x2−2pxy+4p+y2=0
⇒(y−px)2+4p=0
∴y−px=2√−p
⇒y=px+2√−p…(i)
on differentiating w.r.t.x, we get
p=p+dpdx⋅x+2⋅(12)(−P)1/2⋅(−1)dpdx
⇒dpdx{x−(−P)1/2}=0
⇒dpdx=0orx=(−p)−1
If dpdx=0⇒P=c
On putting this value in Eq. (i), we get y=cx+2√−c
This curve passes through (1,1).
⇒1=c+2√−c
⇒c=−1
∴y=−x+2
⇒x+y=2
Again, if x=(−p)−1/2
⇒−p=1x2 putting in Eq. (i)
y=−xx2+2⋅1x⇒xy=1
Thus, the two curves are xy = 1 and x+ y = 2.
Topper's Solved these Questions
- DIFFERENTIAL EQUATIONS Book:IIT JEE PREVIOUS YEARChapter:DIFFERENTIAL EQUATIONS Exercise:TOPIC 1 SOLUTION OF DIFFERENTIAL EQUATIONS BY VARIABLE <br> SEPARATION METHOD <br> INTEGER ANSWER TYPE QUESTION
Explore 1 Video
- DIFFERENTIAL EQUATIONS Book:IIT JEE PREVIOUS YEARChapter:DIFFERENTIAL EQUATIONS Exercise:TOPIC 2 LINEAR DIFFERENTIAL EQUATION AND <br> EXACT DIFFERENTIAL EQUATION <br> OBJECTIVE QUESTIONS I (ONLY ONE CORRECT OPTION)
Explore 21 Videos
- DIFFERENTIAL EQUATIONS Book:IIT JEE PREVIOUS YEARChapter:DIFFERENTIAL EQUATIONS Exercise:TOPIC 1 SOLUTION OF DIFFERENTIAL EQUATIONS BY VARIABLE <br> SEPARATION METHOD <br> NUMERICAL VALUE
Explore 2 Videos
- DEFINITE INTEGRATIONBook:IIT JEE PREVIOUS YEARChapter:DEFINITE INTEGRATIONExercise:LIMITS AS THE SUM
Explore 6 Videos
- ELLIPSEBook:IIT JEE PREVIOUS YEARChapter:ELLIPSEExercise:EQUATION OF CHORD OF CONTACT, CHORD BISECTED AT A GIVEN POINT & DIAMETER
Explore 3 Videos
Similar Questions
The area of the triangle formed by the tangent to the curve xy=a2 at any point on the curve with the coordinate axis is
View SolutionThe triangle formed by the tangent to the curve f(x)=x2+bx−b at the point (1,1) and the coordinate axes lies in the first quadrant. If its area is 2, then the value of b is
View Solution
Knowledge Check
The area of the traingle formed by the coordinate axes and a tangent to the curve xy=a2 at the point (x1,y1) is
Aa2x1y1Ba2y1x1C2a2D4a2Find the value of |a| for which the area of triangle included between the coordinate axes and any tangent to the curve xay=λa is constant (where λ is constnat.),
A1/2B2C3/2D1Equation of the tangent to the curve y=2x2+5x, at the point where the line y=3 cuts the curve in the first quadrant , is
A14x−2y−1=0B14x−2y+13=0C14x+2y−1=0D2x−14y−1=0
The triangle formed by the tangent to the curve f(x)=x2+bx−b the point (1, 1) and the co-ordinate axes, lies in the first quadrant. If its area is 2, then the value of b is
View SolutionThe equation of the curve, passing through (2, 5) and having the area of triangle formed by the X-axis, the ordinate of a point on the curve and the tangent at the point 5 sq.units as
View SolutionA normal at any point (x,y) to the curve y=f(x) cuts a triangle of unit area with the axis, the differential equation of the curve is
View SolutionThe area of the triangle formed by normal at the point (1,0) on the curve x=esiny with axes is
View SolutionThe slope of the tangent to the curve y=x2−x at the point where the line y = 2 cuts the curve in the first quadrant, is
View Solution