Give reasons to show that none of the following expressions is a polynomial.
(i) f(x)=x+1x
(ii) g(x)=√x−3
(iii) h(y)=3√y−6
(iv) p(x)=(x−1)(x−3)x
(v) q(x)=1x+2
(vi) r(x)=x+3x+4
(i) f(x)=x+1x may be written as f(x)=x+x−1.
Here , in one term , the exponent of x is - 1 , which is a negative integer .
∴f(x) is not a polynomial .
(ii) g(x)=√x−3 may be written as g(x) =1/2−3. Here , in one term , the exponent of x is 12 , which is not a non - negative integer .
∴ g (x) is not a polynomial .
(iii) h(y)=3√y−6 may be written as h(y)=y1/3−6. Here , in one term , the exponent of y is 13, which is not a non - negative integer.
∴h(y) is not a polynomial .
(iv) p(x)=(x−1)(x−3)x
⇒p(x)=x2−4x+3x=(x−4+3x)=(x−4+3x−1).
Here , in one term , the exponent of x is -1 , which is a negative integer.
∴p(x) is not a polynomial.
(v) q(x)=1(x+2)=(x+2)−1, which is not a polynomial in (x+2)and therefore , it is not a polynomial in x .
(vi) On dividing (x+3) by (x+4) , we get 1 as quotient and -1 as remainder.
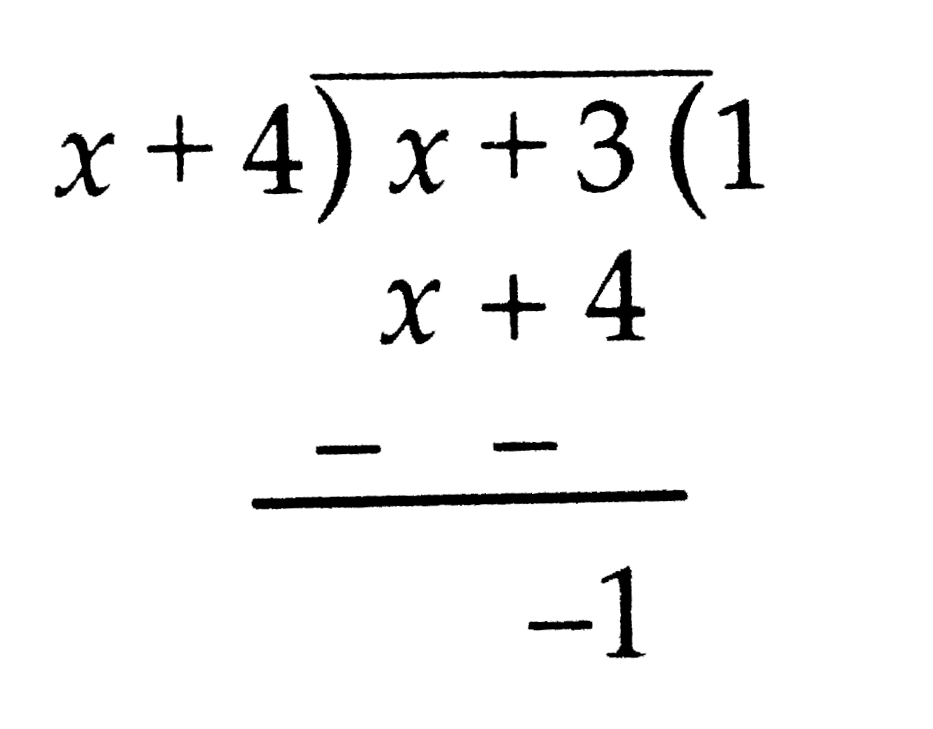
∴ we may write , x+3x+4=1−1(x+4)=1−(x+4)−1, which is not a polynomial .
Hence , r (x)=x+3x+4 is not a polynomial.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - POLYNOMIALSEXERCISE - Exercise 2A6videos
POLYNOMIALS
- BOOK - RS AGGARWALCHAPTER - POLYNOMIALSEXERCISE - Exercise 2B9videos
POLYNOMIALS
- BOOK - RS AGGARWALCHAPTER - NUMBER SYSTEMSEXERCISE - Very Short Answer Questions23videos
NUMBER SYSTEMS
- BOOK - RS AGGARWALCHAPTER - PRESENTATION OF DATA IN TABULAR FORMEXERCISE - Multiple Choice Questions (Mcq)9videos
PRESENTATION OF DATA IN TABULAR FORM
Similar Questions
Find domain(i) f(x)=1x−5 (ii) f(x)=3−xx−3 (iii) f(x)=x2−1x−1 (iv) f(x)=|x−3|x−3 (v) f(x)=12−sin3x
View SolutionWhich of the following are polynomials :
(i) 3x2−7x+6 (ii)x2−√3x+4 (iii)3√x+5 (iv)13 (v)a+5a+6View SolutionWhich of the following algebraic expressions are polynomials?
I. x3+√3x+4 , II. x2+2√x+4
III. x2+√x−1, IV. x2+3x+4View SolutionFind the zero of the polynomial :
(i)p(x)=x−3 (ii)q(x)=3x−4 (iii)p(x)=4x−7 (iv)q(x)=px+q,p≠0
(v)p(x)=4x (vi)p(x)=32x−1View SolutionFind the domain of each of the following real fuctions:
(i) f(x)=√x−3 (ii) g(x)=√4−x2 (iii) h(x)=1√1−x.View Solutionwhich of the following expressions are polynomials ? Justify your answer,
(i) 8 (ii) √3x2−2x<br>(iii)1−√5x
(iv)15x−2+5x+7<br>(v)(x−2)(x−4)x(vi)1x+1
(vii)17a3−2√3a2+4a−7<br>(viii)12xView SolutionWhich of the following are polynomials ?
(i)x2−3x+1 (ii)x2+5x+2 (iii)x−1y (iv)x7+8 (v)x3+√x−2
(vi)√2x2+x−1 (vii)(3x−1)(x+5) (viii)(x−3x)(x+2) (ix)2x2−1
(x)x+1√x+2View SolutionFind the zeroes of the polynomial ineach of the followning .
(i)p(x)=x−4 (ii)g(x)=3−6x
(iii)q(x)=2x−7 (iv)h(y)=2yView SolutionFor what values of x are the following functions not defined ? (i) 3x4x−3 (ii) √x−2 (iii) 1√x−3 (iv) sinxx (v) sin1x (vi) √(x+2)(x−3)
View SolutionVerify whether the following are zeroes of the polynomial, indicated against them.(i) p(x)=3x+1,x=−13 (ii) p(x)=5x−π,x=45 (iii) p(x)=x2−1,x=1,−1(iv) p(x)=(x+1)(x+2),x=−1,2 (v) p(x)=x2,x=0 (vi) p(x)=lx+m,x=−ml
View Solution


