In the given figure C is the midpoint of AB,D is the midpoint of XY and AC=XD Using an Euclid 's axiom prove that AB =XY
To prove that AB=XY given that C is the midpoint of AB, D is the midpoint of XY, and AC=XD, we will follow these steps:
Step 1: Understand the Midpoints
Since C is the midpoint of AB, we can express the lengths as:
AC=12ABandCB=12AB
Similarly, since D is the midpoint of XY, we can express the lengths as:
XD=12XYandDY=12XY
Step 2: Express AB and XY in terms of AC and XD
From the definitions of midpoints:
AB=AC+CB=AC+AC=2AC
XY=XD+DY=XD+XD=2XD
Step 3: Use the Given Information
We are given that AC=XD. Therefore, we can substitute XD with AC in the equation for XY:
XY=2XD=2AC
Step 4: Conclude the Proof
Now we have:
AB=2ACandXY=2AC
Since both AB and XY are equal to 2AC, we can conclude that:
AB=XY
Final Statement
Thus, we have proven that AB=XY.
---
Since C is the midpoint of AB, we can express the lengths as:
AC=12ABandCB=12AB
Similarly, since D is the midpoint of XY, we can express the lengths as:
XD=12XYandDY=12XY
From the definitions of midpoints:
AB=AC+CB=AC+AC=2AC
XY=XD+DY=XD+XD=2XD
We are given that AC=XD. Therefore, we can substitute XD with AC in the equation for XY:
XY=2XD=2AC
Now we have:
AB=2ACandXY=2AC
Since both AB and XY are equal to 2AC, we can conclude that:
AB=XY
Thus, we have proven that AB=XY.
Topper's Solved these Questions
- INTRODUCTION TO EUCLID'S GEOMETRYBook:RS AGGARWALChapter:INTRODUCTION TO EUCLID'S GEOMETRYExercise:Example
Explore 1 Video
- INTRODUCTION TO EUCLID'S GEOMETRYBook:RS AGGARWALChapter:INTRODUCTION TO EUCLID'S GEOMETRYExercise:Exercise
Explore 6 Videos
- GEOMETRICAL CONSTRUCTIONSBook:RS AGGARWALChapter:GEOMETRICAL CONSTRUCTIONSExercise:Exercise 13
Explore 2 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBook:RS AGGARWALChapter:LINEAR EQUATIONS IN TWO VARIABLESExercise:Multiple Choice Questions (Mcq)
Explore 24 Videos
Similar Questions
Knowledge Check
In triangle ABC,D is the midpoint of AB, E is the midpoint of DB and F is the midpoint of BC. If the area of ΔABC is 96, the area of ΔAEF is
A16B24C32D36
In the following figures, PQ = LM, Q is the midpoint of PR and M is the midpoint of LN. Using the axioms, prove that PR = LN.

View SolutionIn the given figure, AB=AC. prove that :
View SolutionIn the given figure if AC=BD then prove that AB=CD
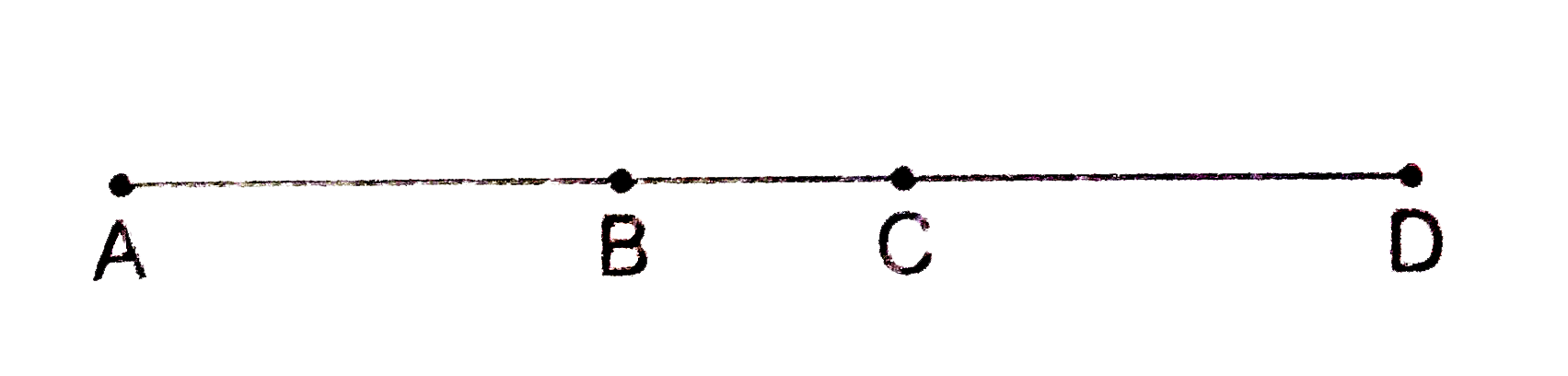
View SolutionIn the given figure, if DE || AC , then AB =
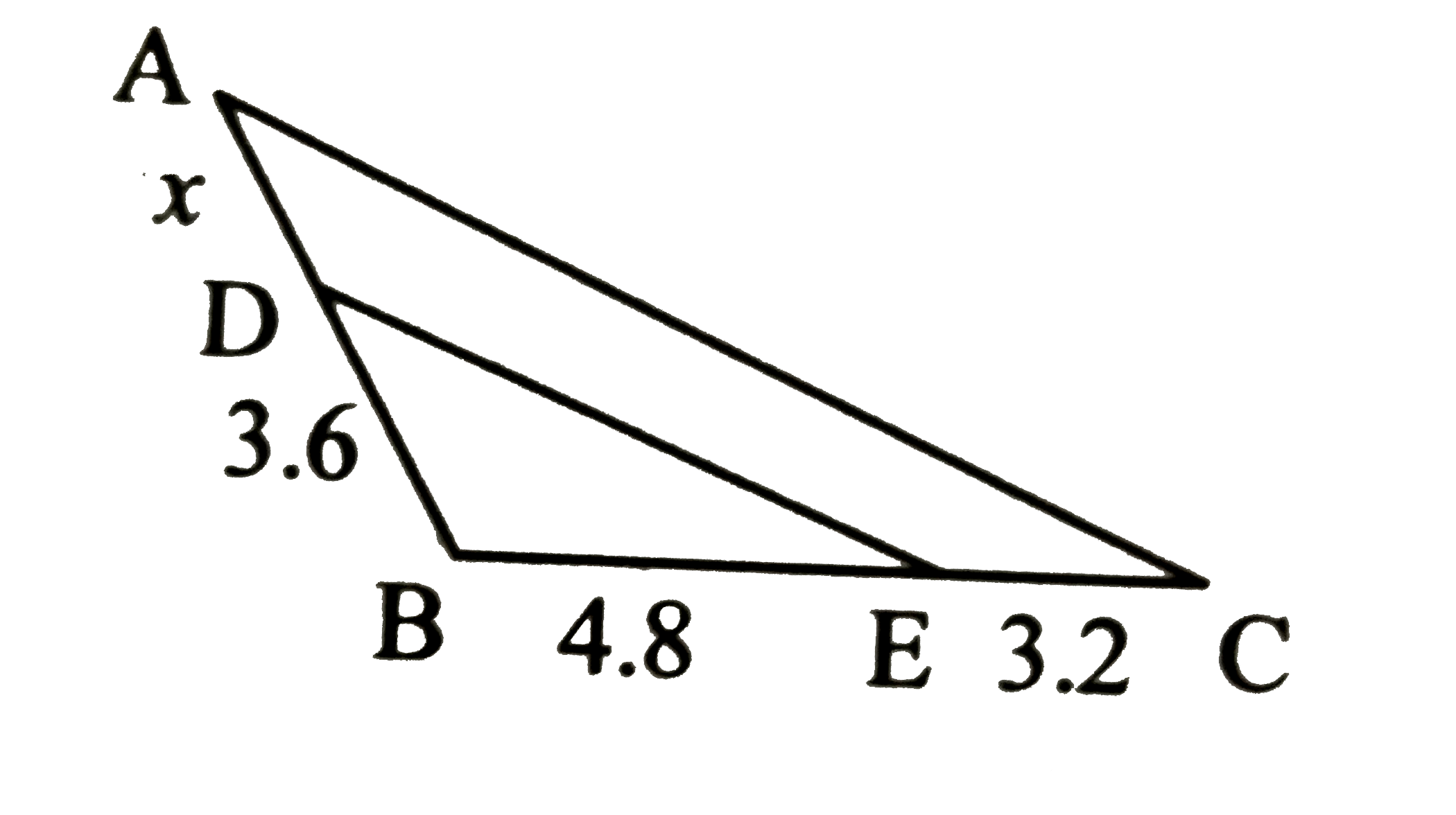
View SolutionIn the given figure , C is the midpoint of AB, if ∠DCA=∠ECBand∠DBC=∠EAC , Prove that DC=EC and BD=AE
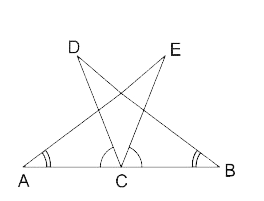
View SolutionIn the given figure, if AC = BD, then prove that AB = CD.

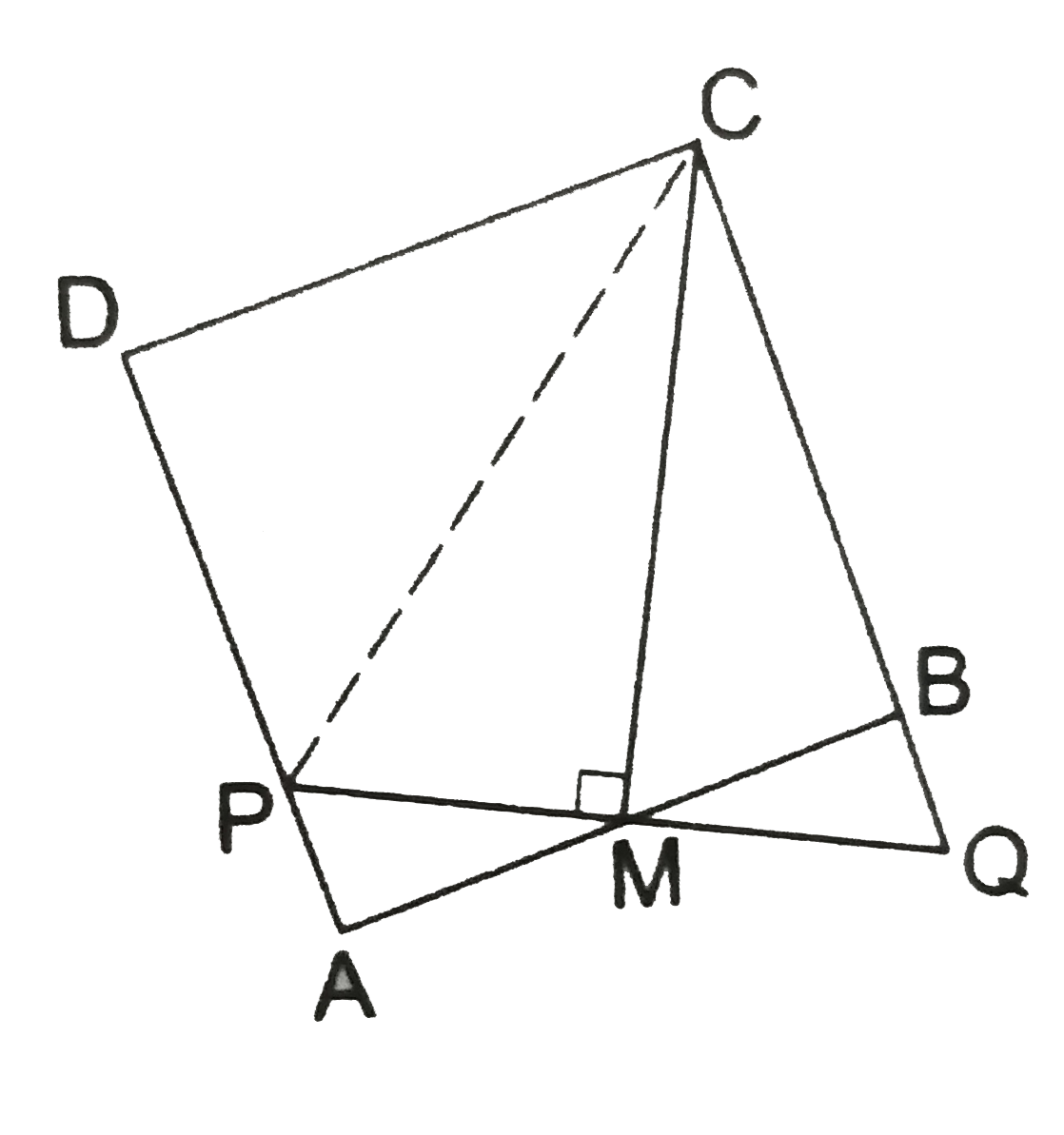
View SolutionIn the given figure, ABCD is a square, M is the midpoint of AB and PQ⊥CM meets AD at P and CB produced at Q. Prove that (i) PA = QB and (ii) CP=AB+PA.
View Solution