In the given figure ΔABC is right angle at A with AB=6 cm and AC=8 cm. A circle with centre O has been inscribed inside the triangle. Find the value of r, the radius of the inscribed circle.
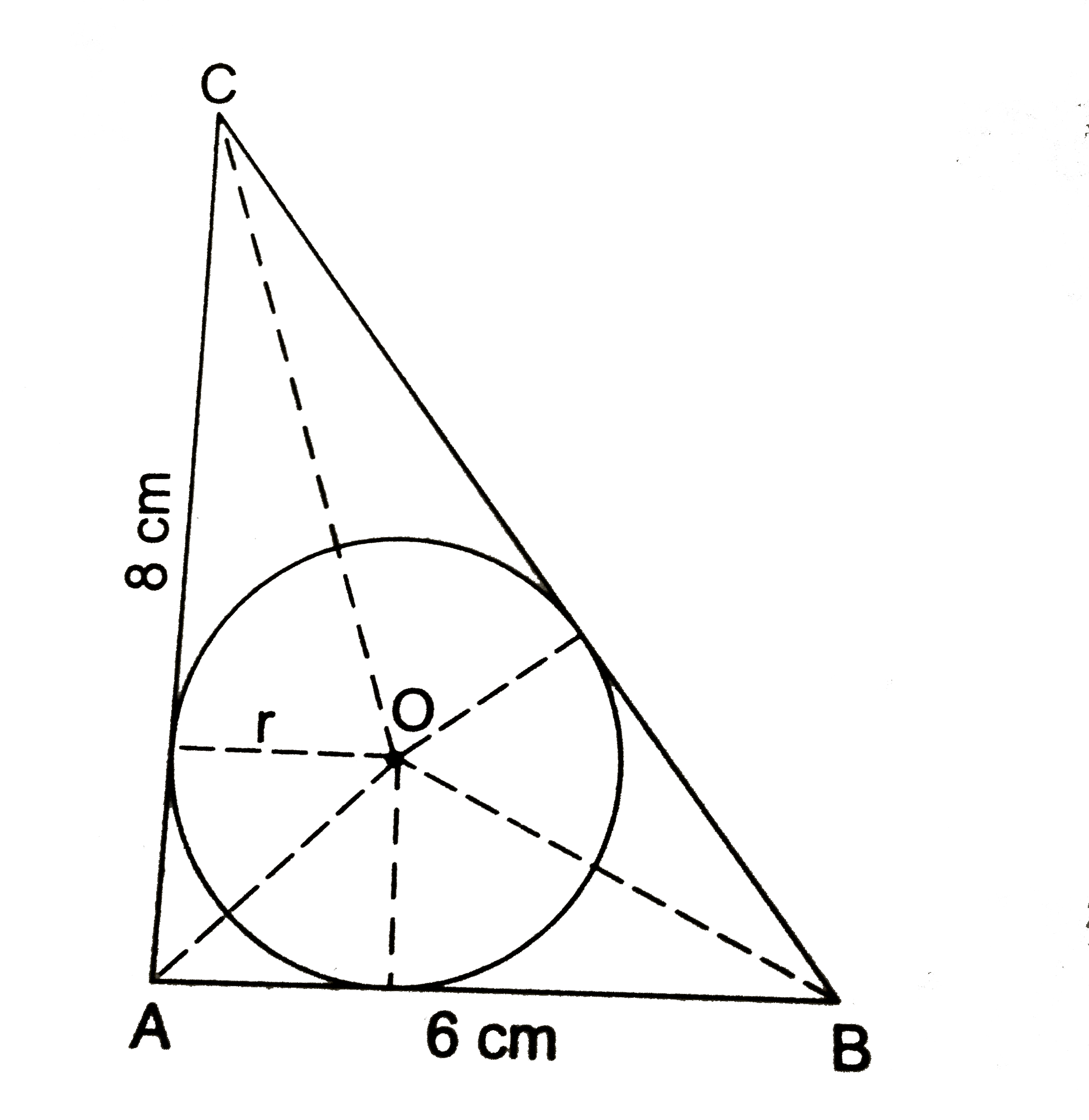
BC=√AB2+AC2=√62+82
=√36+64=√100=10cm
Let O be the centre of the inscribed circle and r be its radius.
Join OA, OB and OC.
ar(ΔOAC)+ar(ΔOAB)+ar(ΔBOC)=ar(ΔABC)
⇒(12×8×r)+(12×6×r)+(12×10×r)=12×6×8
⇒(4r+3r+5r)=24⇒12r=24⇒r=2cm
Hence r=2cm
Topper's Solved these Questions
- AREA OF CIRCLE, SECTOR AND SEGMENT BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - SOLVED EXAMPLE_TYPE
1 Videos
- AREA OF CIRCLE, SECTOR AND SEGMENT BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - Exercise 16A
65 Videos
- ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
Similar Questions
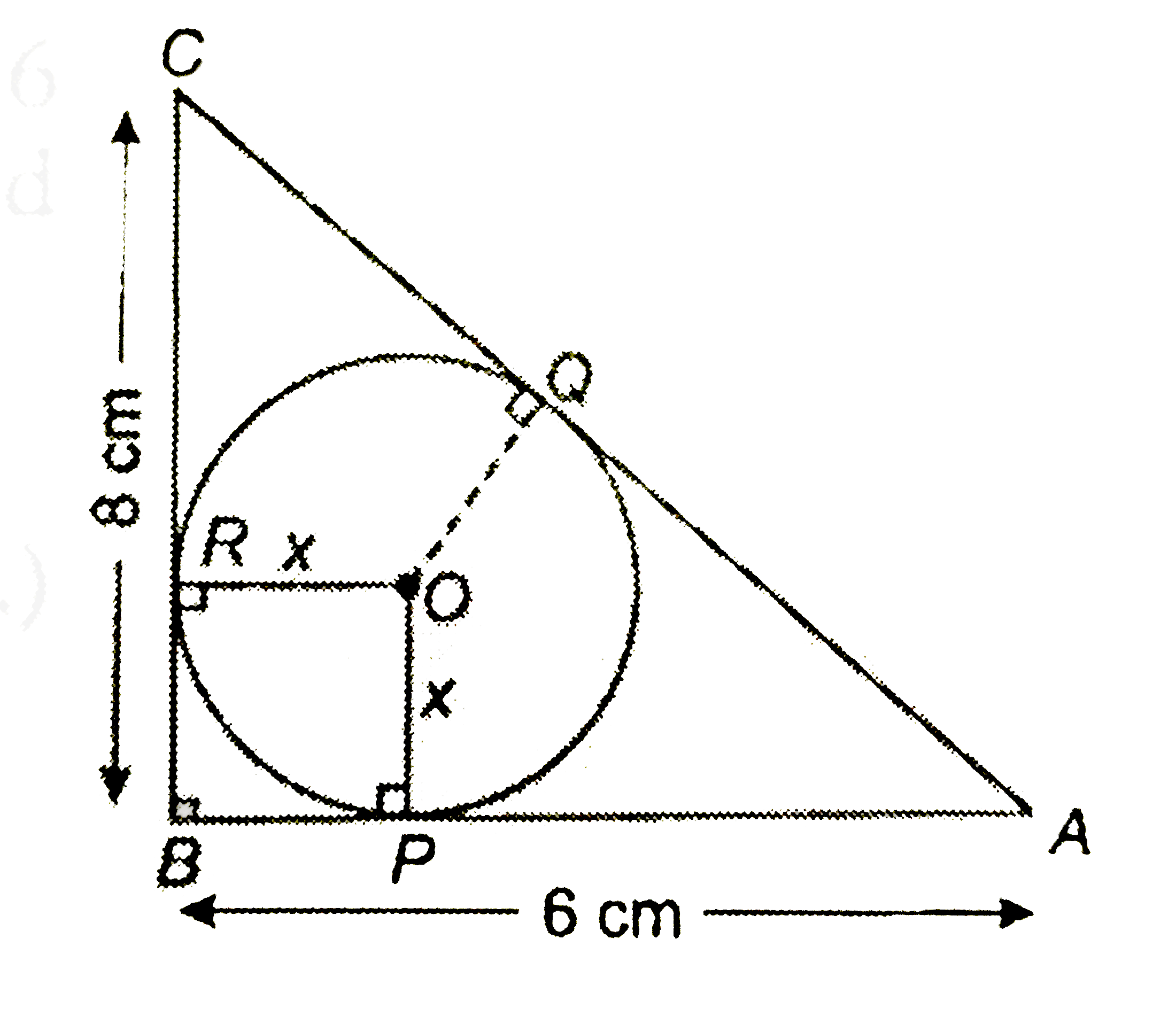
In the given figure ABC is a right angled triangle with AB=6 cm, and BC=8 cm. A circle with centre O has been inscribed inside the triangle. Find the radius of the circle.
View SolutionPQR is a right angled triangle at Q with QR =12 a=cm and PQ=5cm. A circle with centre O is inscribed in △PQR. Find the radius of the circle.
View Solution
Knowledge Check
ABC is a right-angled triangle with AB = 6 cm and BC = 8 cm. A circle with centre O has been in scribed inside ΔABC. The radius of the circle is
A1 cmB2 cmC3 cmD4 cmΔABC is right angled triangled with AB=6 cm, BC=8cm. O is the in centre of the triangle.The ratius of the in -circle is :
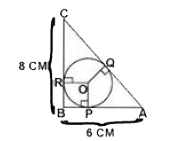 A2cmB5cmC4cmD3cm
A2cmB5cmC4cmD3cmIn a right triangles ABC right angled at B,BC = 12 cm and AB = 5 cm . The radius of the circle inscribed in the triangle (in cm) is
A4B3C2D1
ΔABC is a right angled triangle with ∠A=900AB=bcm,AC=acm,andBC=ccmAcircle is inscribed in this triangle. The radius of the circle,in cm, is:
View SolutionIn triangle ABC,right angled at B, BC = 24 cm, and AB = 7 cm. A circle is inscribed in triangle ABC. Then the radius of the circle is:
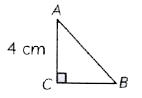
View SolutionIn the given figure, △ABC is an isosceles triangle right angled at C with AC = 4 cm. Find the length of AB.
View SolutionIn the given figure,ABC is a right angled triangle in which ∠A=90∘,AB=21 cm and AC=28 cm.Semi-circles are drawn on AB, BC and AC as diameters. Find the area of shaded region.
View SolutionIn the given figure, in a right angle triangle ABC, AB=12cm and AC=15cm. A square is inscribed in the triangle. One of the vertices of square coincides with the vertex of triangle. What is the maximum possible area (in cm2) of the square ?
View Solution
