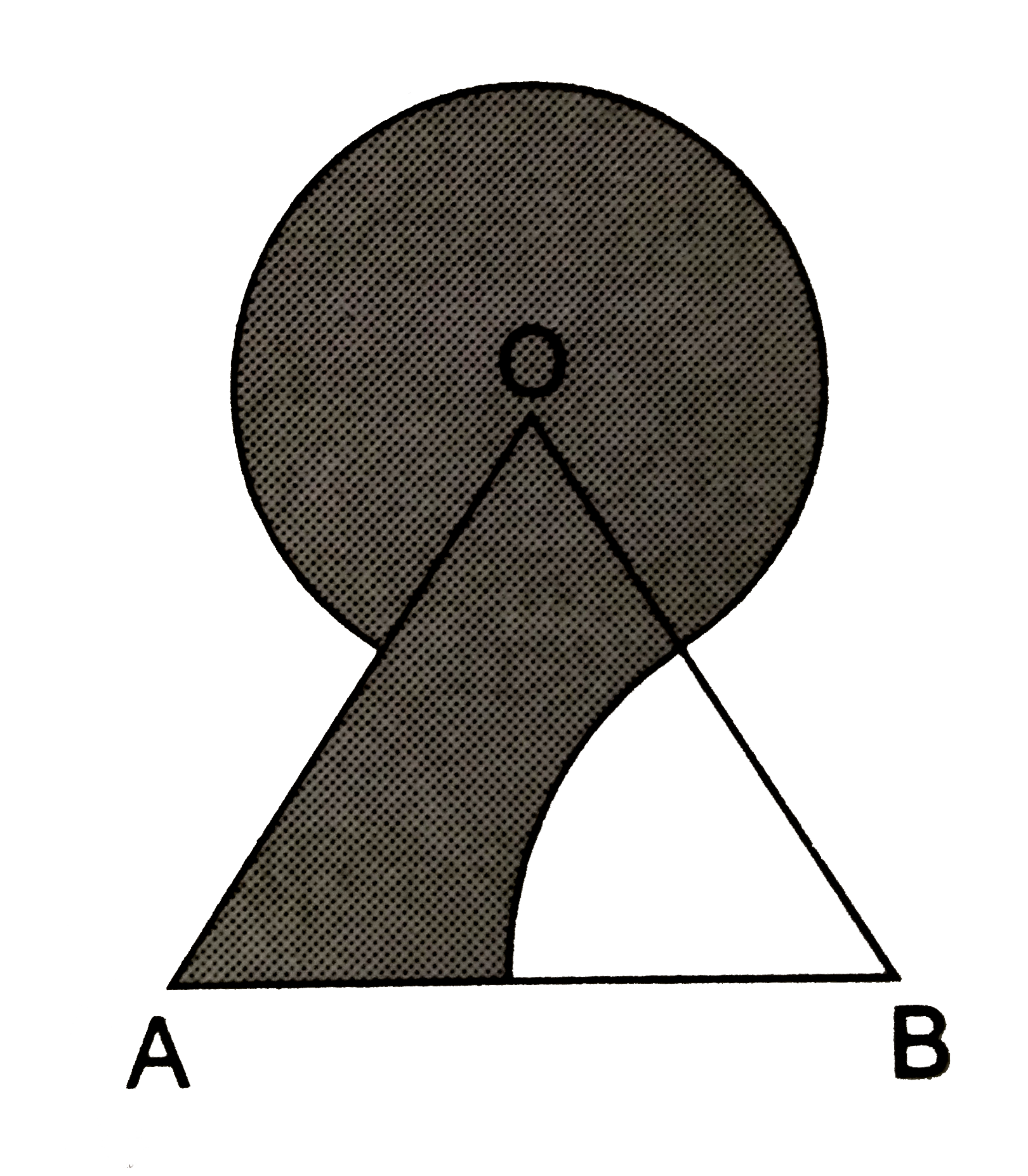
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex $O$ of an equilateral triangle OAB of side 12 cm as centre.
[ Take $\sqrt{3} = 1.73$ and $π = 3.14$ ]

Video Solution

Text Solution

Verified by Experts

Since $Δ O A B$ is equilateral, we have $∠ A O B = 60^{\circ}$
Required area
$= {(area of equilateral Δ O A B) + (area of circle with r = 6 c m)}$
$- (area of sector of a circle with r = 6 c m and θ = 60^{\circ})$
$= {(\frac{\sqrt{3}}{4} \times 12 \times 12) + (π \times 6 \times 6) - (π \times 6 \times 6 \times \frac{60}{360})} c m^{2}$
$= {(1.73 \times 36) + 36 π - 6 π} c m^{2} = {(1.73 \times 36) + (30 π)} c m^{2}$
$= {(\frac{173}{100} \times 36) + (30 \times \frac{314}{100})} c m^{2} = (\frac{1557}{25} + \frac{471}{5}) c m^{2}$
$= (\frac{1557 + 2355}{25}) c m^{2} = 3912 c m^{2} = 156.48 c m^{2}$
Hence the area of the shaded region is $156.48 c m^{2}$

|

Updated on:21/07/2023

Class 10 MATHS AREAS RELATED TO CIRCLES

Topper's Solved these Questions

Similar Questions

RS AGGARWAL-AREA OF CIRCLE, SECTOR AND SEGMENT -Test Yourself

Home
Ask Doubt
Profile