An arch is in the form of a parabola with its axis vertical. The arch is 10 m high and 5 m wide at the base. How wide is it 2 m from the vertex of the parabola?

Video Solution

Text Solution

Verified by Experts

Let O be the origin and OY be the vertical axis of the parabolic arch.

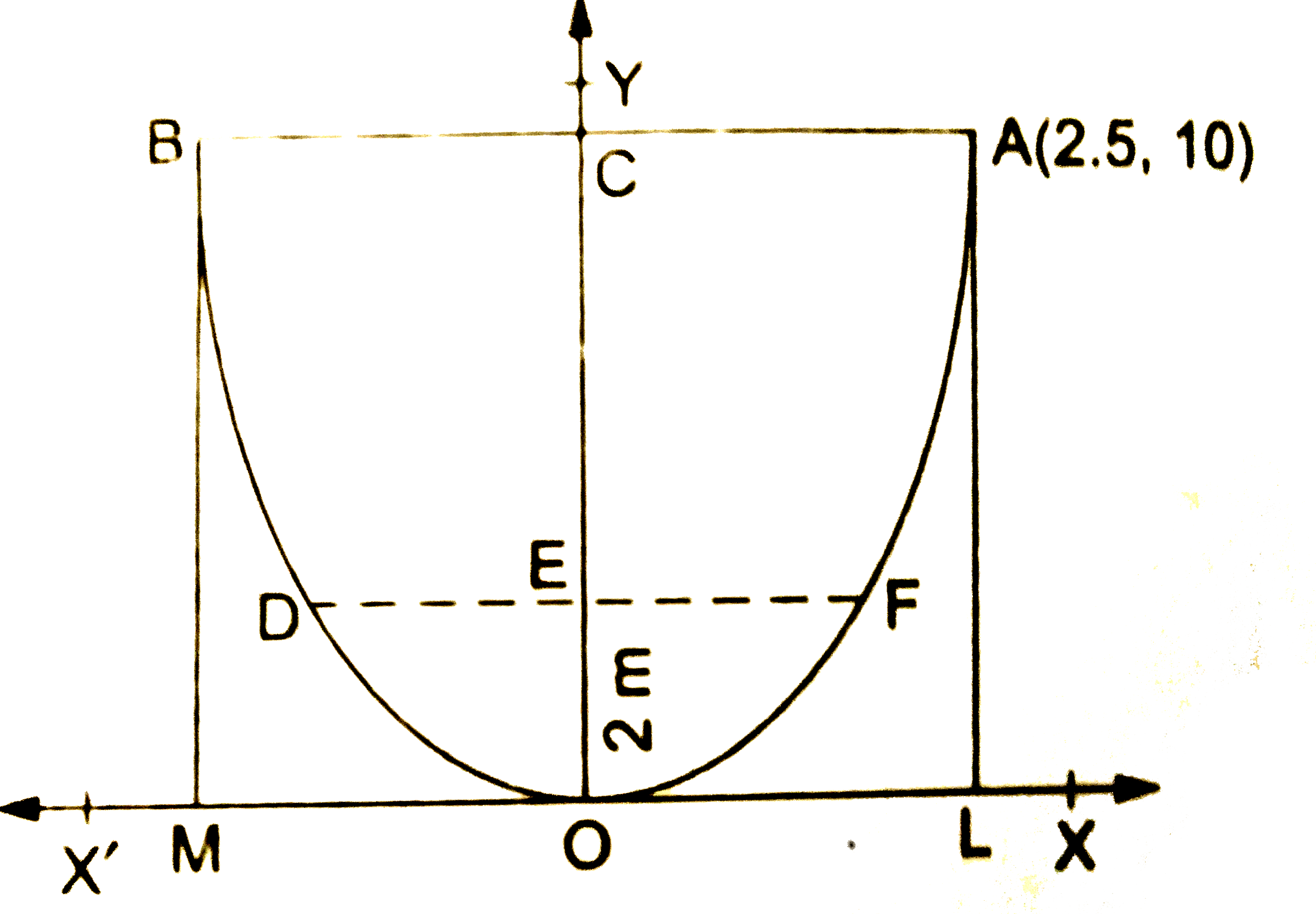
Then, the equation of the arch is
$x^{2} = 4 a y .$ …(i)
$∴ B A = 5 m and O C = 10 m .$
Noe, $O L = \frac{1}{2} M L = \frac{1}{2} B A = 25 m$ .
And , $A L = O C = 10 m .$
$∴$ the coordinates of A are $(2.5, 10) .$ Since A(25, 10) lies on (i) , we have
${(2.5)}^{2} = 4 a \times 10 \Rightarrow a = (\frac{2.5 \times 2.5}{4 \times 10}) = \frac{5}{32} .$
$∴ x^{2} = (4 \times \frac{5}{32} \times y) \Rightarrow x^{2} = \frac{5}{8} y .$ ....(ii)
Draw DEF|| ML such that OE = 2 m.
Let the coordinates of F be $F (x_{1}, 2)$ .
Since $F (x_{1}, 2)$ lies on (ii), we have
$x_{1}^{2} = (\frac{5}{8} \times 2) \Rightarrow x_{1}^{2} = \frac{5}{4} \Rightarrow x_{1} = \frac{\sqrt{5}}{2} .$
$∴ E F = \frac{\sqrt{5}}{2} m \Rightarrow D F = 2 \times E F = (2 \times \frac{\sqrt{5}}{2}) m = \sqrt{5} m .$
Hence, the required width of the arch at a distance at a distance of 2 m from its vertex is $\sqrt{5}$ metres.

Updated on:21/07/2023

A rectangular park is 100 m long and 60 m wide. There is a path 2 m wide out side the park. Find the area of the path?
A $324 m^{2}$
B $656 m^{2}$
C $675 m^{2}$
D $780 m^{2}$
In a model, it is shown that an arc of a bridge in semi-elliptical with major axis horizontal. If the length of the base is 9 m and the highest part of the bridge is 3 m from the horizontal, the best approximation of the height of the arch at 2 m from the centre of the base is
A11/4 m
B8/3 m
C7/2 m
D2 m