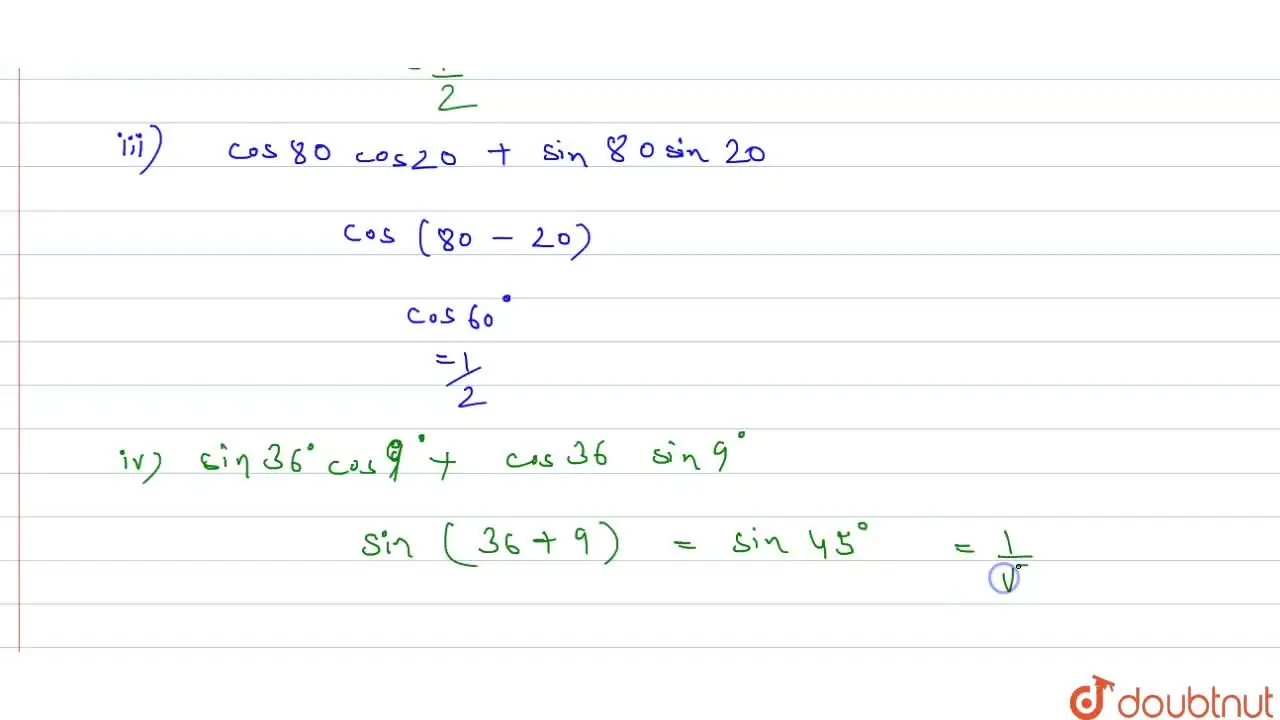Prove that
(i) sin 70∘cos10∘−cos70∘sin10∘=√32
(ii) cos 50∘cos10∘−sin50∘sin10∘=12
(ii) cos 80∘cos20∘+sin80∘sin20∘=12
(iv) sin 36∘cos9∘+cos36∘sin9∘=1√3
(i) We know that the sin θ cos ϕ=− cos θ sin ϕ= sin (θ−ϕ)
Putting θ=70∘ and ϕ=10∘ in the this identity we get
sin70∘cos 10∘−cos 70∘sin 10∘=sin 70∘−10∘=sin 60∘=√32
(ii) We know that cos θ cos ϕ - sin θ sin ϕ=cos (θ+ϕ)
Putting θ=50∘and ϕ=10∘ in the this identity we get
cos 50∘cos10∘=sin50∘sin10∘=cos50∘+10∘=cos60∘=12
(iii) We know that cos θ cos ϕ+sin ϕ=cos (θ−ϕ)
Putting θ=80∘and ϕ=20∘ in this dientity we get
cos 80∘cos 20∘+sin 80∘sin 20∘=cos (80∘−20∘)=cos 60∘=12
(iv) We know that sin θsin θ cos ϕ+cos θ sin ϕ=cos (θ+ϕ)
Putting θ=36∘ and ϕ=9∘in this identity , we get
sin 36∘cos 9∘+cos 36∘sin 9∘=sin (36∘+9∘)=sin 45∘=1√2
Related Playlists
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC , OR CIRCULAR, FUNCTIONSEXERCISE - Exercise (15A)10videos
TRIGONOMETRIC , OR CIRCULAR, FUNCTIONS
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC , OR CIRCULAR, FUNCTIONSEXERCISE - Exercise (15B)20videos
TRIGONOMETRIC , OR CIRCULAR, FUNCTIONS
- BOOK - RS AGGARWALCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - EXERCISE 26 C13videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - EXERCISE21videos
TRIGONOMETRIC EQUATIONS
Similar Questions
Show that sin700cos100−cos700sin100=√32
View SolutionProve that
(i) sin 80∘cos 20∘− cos 80∘ sin 20∘=√32
(ii) cos 45∘ cos 15∘− sin 45∘ sin 15∘=12
(iii) cos 75∘ cos 15∘+ sin 75∘ sin 152=12
(iv) sin 40∘ cos 20∘ + cos 40∘ sin 20∘=√32
(v) cos 130∘ cos 40∘l+ sin 130∘ sin 40∘=0View SolutionShow that : cos700.cos100+sin700.Sin100=12
View SolutionProve that (sin20∘+sin40∘)+(cos20∘+cos40∘)=(√3+1)cos10∘
View Solutioncos20∘+8sin70∘sin50∘sin10∘sin280∘ is equal to
View SolutionEvaluate the following: cos800cos200+sin800sin200
View Solutionsin10∘+sin20∘+sin40∘+sin50= A)sin15∘+sin75∘B)cos15∘+cos75∘C)sin70∘+sin80∘D)cos70∘+cos80∘
View Solutioncos20∘+8sin70∘.sin50∘.sin10∘sin2(80)∘
View Solution12sin10∘−√32cos10∘
View SolutionThe value of sin10∘cos80∘+cos10∘sin80∘ is
View Solution