Two concentric circular coil,s one of small radius r1 and the other of large radius r2, such that r1<<r2, are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.Solution in Tamil
Let a current I2 flow through the outer circular coil. The field at the centre of the coil is B2=μ0I2/2r2 . Since the other co-axially placed coil has a very small radius, B2 may be considered constant over its cross-sectional area. Hence,
Φ1=πr21B2
=μ0πr212r2I2
M12I2
Thus,
M12=miu0πr212r2
From Eq. (6.14)
M12=M21=μ0πr212r2
Note that we calculated M12 from an approximate value of Φ1
, assuming the magnetic field B2 to be uniform over the area πr21. However, we can accept this value because r1<<r2.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:NCERT TAMILChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISES
Explore 10 Videos
- ELECTROMAGNETIC INDUCTIONBook:NCERT TAMILChapter:ELECTROMAGNETIC INDUCTIONExercise:ADDITIONAL EXERCISES
Explore 7 Videos
- ELECTRIC CHARGES AND FIELDS Book:NCERT TAMILChapter:ELECTRIC CHARGES AND FIELDS Exercise:EXERCISES
Explore 34 Videos
- ELECTROMAGNETIC WAVESBook:NCERT TAMILChapter:ELECTROMAGNETIC WAVESExercise:Evaluation (Numerical problems)
Explore 5 Videos
Similar Questions
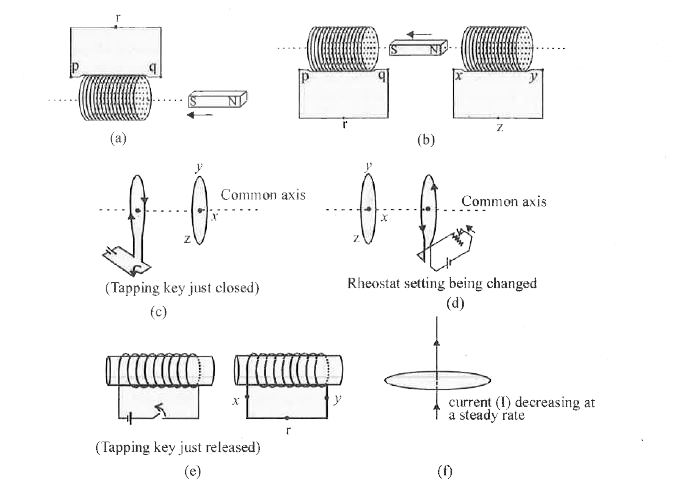
Predict the direction of induced current in the situations described by the following figures (a) to (f).
View SolutionSuppose the loop in Textual Exercise 4 is stationary but the current feeding the electromagnet that produces the magnetic field is gradually reduced so that the field decreases from its initial value of 0.3 T at the rate of 0.02Ts−1 .If the cut is joined and the loop has a resistance of 1.6Ω how much power is dissipated by the loop as heat ? What is the source of this power ?
View SolutionWhat is the force between two small charged spheres having charges of 2×10−7Cand3×10−7C placed 30cm apart in air ?
View SolutionConsider a parallel plate capacitor whose plates are closely spaced. Let R be the radius of the plates and the current in the wire connected to the plates is 5 A, calculate the displacement current through the surface passing between the plates by directly calculating the rate of change of flux of electric field through the surface.
View SolutionIn co-axial concentric coils of radius r_(1) and r_(2) such that r_(1) lt lt r_(2) Fig. find direction of induced current when K is (i) pressed (ii) released.
View SolutionTwo circular coils, one of smaller radius r1 and the other of very large radius r2 are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View SolutionTwo coils are placed closed to each other. The mutual inductance between them assuming R_(2)lt ltR_(1)
View SolutionTwo concentric circular coil,s one of small radius r1 and the other of large radius r2, such that r1<<r2, are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View Solution(a) Explain the meaning of the term mutual inductance. Consider two concentric circular coils, one radius r_(1) and the other of radius r_(2)(r_(1) lt r_(2)) placed coaxially with centres coinciding with each other. Obtain the expression for the mutual inductance of the arrangement. (b) A rectangular coil of area A , having number of turns N is rotated at 'f' revoluation per second in a uniform magnetic field B , the field being perpendicular to the coil. Prove that maximum emf induced in the coil is 2pifNBA .
View Solutionदो संकेद्रीय (concentric ) वृत्ताकार कुंडलियाँ समाक्षीय रुप से (coaxially) व्यवस्थित हैं । इनकी त्रिज्याएँ r1 तथा (r2 हैं तथा r1≤≤r2 हैं । इस अवस्था का अन्योन्य प्रेरकत्व (mutual inductance) ज्ञात करें ।

View SolutionTwo concentric circular coil,s one of small radius r1 and the other of large radius r2, such that r1<<r2, are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View Solutionदो संकेंद्रित वृताकार कुंडलिया एक कम त्रिजिया r1 की तथा दूसरी अधिक त्रिजिया r2 की ऐसे की r1>>r2 समाक्षी रखी है था दोनों के केंद्र संपत्ति है इस व्यवस्था के लिए अन्यों परिकत्व ज्ञात कीजिये
View SolutionTwo concentric circular coils, one of small radius r1 and the other of large radius r2, such that r1<<r2, are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View SolutionTwo concentric circular coils, one of small radius r1 and the other of large radius r2, such that r1<<r2, are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View SolutionTwo circular coils, one of smaller radius r_(1) and the other of very large radius r_(2) are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View SolutionTwo concentric circular coils, one of small radius r1 and the other of large radius r2, such that r1<<r2, are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.

View Solution