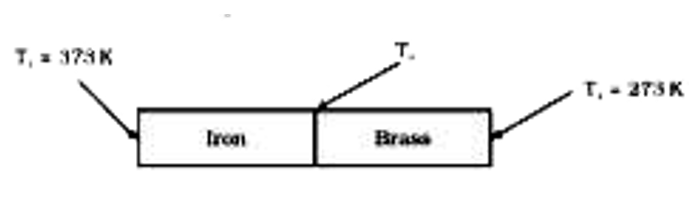
An iron bar (L1=0.1m,A1=0.02m2,K1=79Wm−1K−1) and a brass bar (L2=0.1m,A2=0.02m2,K2=109Wm−1K−1) are soldered end to end as shown in Fig. 11.16. The free ends of the iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (1) the temperature of the function of the two bars, (11) the equivalent thermal conductivity of the compound bar, and (111) the heat current through the compound bar.
 Solution in Tamil
Solution in Tamil
Given, L1=L2=L=0.1m,A1=A2=A=0.02m2K1=79Wm−1K−1,K2=109Wm−1K−1,T1=373K, and T2=273K.
Under steady state condition, the heat current (H1) through iron bar is equal to the heat current (H2) through brass bar.
So, H=H1=H2=(K1A1T1−T0L1)=(K2A2T0−T2L2)
For A1=A2=A and L1=L2=L, this equation leads to
K1(T1−T0)=K2(T0−T2)
Thus , the junction temperature T0 of the two bars is T0=(K1T1+K2T2(K1+K2))
Using this equation, the heat current H through either bar is
H=K1A(T1−T0)L=K2(T0−T2)L=(K1K2K1+K2)A(T1−T2)L(1K1+1K2)
Using these equations, the heat current H. through the compound bar of length L1+L2=2L and the equivalent thermal conductivity K. , of the compound bar are given by
H. = K.A(T1−T2)2L=H
K.=2K1K2K1+K2
(i) T0=(K1T1+K2T2)(K1+K2)
=(79Wm−1K−1)(373K)+(109Wm−1K−1)(273K)79Wm−1K−1+109Wm−1K−1
=315K
(ii) K.=2K1K2K1+K2
=2×(79Wm−1K−1)×(109Wm−1K−1)79Wm−1K−1+109Wm−1K−1
=91.6Wm−1K−1
(iii)H.=H=K.A(T1−T2)2L
=(91.6Wm−1K−1)×(0.02m2)×(373K−273K)2×(0.1m)
=916.1W
Topper's Solved these Questions
- THERMAL PROPERTIME OF MATTERBOOK - NCERT TAMILCHAPTER - THERMAL PROPERTIME OF MATTEREXERCISE - EXERCISES
31 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - NCERT TAMILCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISES (TRUE OR FALSE)
5 Videos
- THERMODYNAMICS BOOK - NCERT TAMILCHAPTER - THERMODYNAMICS EXERCISE - EXERCISES
10 Videos
Similar Questions
The triple point of neon and carbon dioxide are 24.57K and 216.55K respectively. Express these temperature on the Celsius and Fahrenheit scales.
View SolutionRead each statement below carefully and state with reasons, if it is true ot false. (a) During rolling the force of friction acts in the same direction as the direction of motion of c.m of the body. (b) The instantaneous speed of the point of contact during rolling is zero. (c ) The instantaneous acceleration of the point of contact during rolling is zero. (d) For perfect rolling motion, work done against friction is zero. (e) A wheel moving down a perfectly frictionless inclined plane will undergo slipping (not rolling motion).
View SolutionA boiler heats water flowing at the rate of 2,0 litres per minute from 27°C to 77°C. If the boiler operates on a gas burner, the rate of consumption of the fuel if its heat of combustion is 4.0×104J/g , is
View SolutionAn iron bar ( L_(1) = 0.1 m, A_(1) = 0.02 m^(2) , K_(1) = 79 Wm^(-1) K^(-1) ) and a brass bar (L_(2)=0.1 m , A_(2) = 0.02 m^(2), K_(2) = 109 Wm^(-1)K^(-1) ) are soldered end to end as shown in fig. the free ends of iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the juction of the two bars, (ii) the equivalent thermal conductivity of the compound bar and (iii) the heat current through the compound bar. .
View SolutionIf L1=(3.03±0.02)m and L2=(2.01±0.02)m then L1+2L2 in (in m)
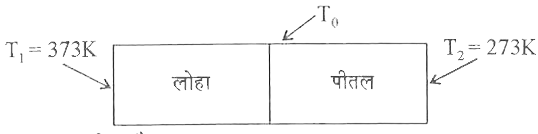
View Solutionचित्र 11.16 में दर्शाए अनुसार लोहे की किसी छड़ (L1=0.1m,A1=0.02m2,K1=79Wm−1K−1) को किसी पीतल की छड़ (L2=0.1m,A2=0.02m2,K2=109Wm−1K−1) के साथ सिरे से सिरे को मिलाकर डाला गया है | लोहे की छड़ तथा पीतल की छड़ के स्वतंत्र सिरों की क्रमशः 373 K तथा 273 K पर स्थापित किया गया है | (i) दोनों छड़ों की संधि पर ताप, (ii) संयुक्त छड़ की तुल्य ऊष्मा चालकता, तथा (iii) संयुक्त छड़ में ऊष्मा प्रवाह की दर के लिए व्यंजक निकालिए तथा परिकलित कीजिए |
View Solutionif 5x2+2x3+x=A1x+A2x+A3x2+1,then(A1,A2,A3)=
View Solutionयदि ¯a=l1¯i+m1¯j+n1¯k और ¯b=l2¯i+m2¯j+n2¯k दो मात्रक सदिश हों तथा इनके बीच का कोण θ हो, तो दर्शाइए कि
cosθ=l1l2+m1m2+n1n2.
View Solutionचित्र में दर्शाए अनुसार लोहे की किसी छड़ (L1=0.1 m ,A1=0.02m2,K1=79Wm−1K−1) को किसी पीतल की छड़ (L2 0.1 m ,A2=0.02m2,K2=109Wm2K−1) के साथ सिरे को मिलाकर ढाला गया है | लोहे की छड़ तथा पीतल की छड़ के स्वतंत्र सिरों को क्रमशः 373 K तथा 273 K पर स्थापित किया गया है |
दोनों छड़ो की संधि पर ताप
View Solutionलोहे की किसी छड़ (L1=0.1 m ,A1=0.02m2,K1=79Wm−1K−1) को किसी पीतल की छड़ (L2 0.1 m ,A2=0.02m2,K2=109Wm2K−1) के साथ सिरे को मिलाकर ढाला गया है | लोहे की छड़ तथा पीतल की छड़ के स्वतंत्र सिरों को क्रमशः 373 K तथा 273 K पर स्थापित किया गया है |
संयुक्त छड़ की तुल्य ऊष्मा चालकता क्या होगी?
View Solutionलोहे की किसी छड़ (L1=0.1 m ,A1=0.02m2,K1=79Wm−1K−1) को किसी पीतल की छड़ (L2 0.1 m ,A2=0.02m2,K2=109Wm2K−1) के साथ सिरे को मिलाकर ढाला गया है | लोहे की छड़ तथा पीतल की छड़ के स्वतंत्र सिरों को क्रमशः 373 K तथा 273 K पर स्थापित किया गया है |
संयुक्त छड़ में ऊष्मा प्रवाह की दर के लिए व्यंजक निकालिए तथा परिकलित कीजिए |
View Solutionचित्र में दर्शाए अनुसार लोहे की किसी छड़ (L1=0.1m,A1=0.02m2,K1=79Wm−1K−1) को किसी पीतल की छड़ (L2=0.1m,A2=0.02m2,K2=109Wm−1K−1) के साथ सिरे से सिरे को मिलाकर डाला गया है । लोहे की छड़ के तथा पीतल की छड़ के स्वतंत्र सिरों को क्रमशः 373K तथा 273 K पर स्थापित किया गया है। (i) दोनों छड़ों की संधि पर ताप (ii) संयुक्त छड़ की तुल्य ऊष्मा चालकता, तथा (iii) संयुक्त छड़ मे ऊष्मा प्रवाह की दर के लिए व्यंजक निकालिये तथा परिकलित कीजिए।
View SolutionFor the process H2O(l)(1bar,373K)→H2O(g)(1bar,373K) the correct set of thermodynamic parameters is
View SolutionIf the sum of 12+(12+22)…m terms =m(m+1)6k then k is equal to
View Solution¯a=2¯i+5¯j+¯k, ¯b=4¯i+m¯j+n¯kలు నకేఖీయ సదిశలైతే, m, n లను కనుక్కోండి.
View Solution
